
分析 甲、乙、丙等5人站成一排,共有A55=120种,甲、乙均不与丙相邻的情况分类解决,丙如果与两人相邻则,一定是丁和戊,而丁和戊可交换位置共有两种,则丙和丁戊共同构成3人一团,丙如果在首末两位,则有两种选择与丙相邻的只有丁和戊,根据分类和分步原理得到结果,再根据概率公式计算即可.
解答 解:甲、乙、丙等5人站成一排,共有A55=120种,
甲、乙均不与丙相邻的情况为:丙如果与两人相邻则一定是丁和戊,
而丁和戊可交换位置共有两种,则丙和丁戊共同构成3人一团,
从五个位置中选3个相邻的位置共有3种方法,而甲乙可互换又有两种,则有2×3×2=12,
丙如果在首末两位,则有两种选择与丙相邻的只有丁和戊,
其余的三个位置随便排A33种结果根据分步计数原理知共有2×2×1×2×3=24
根据分类计数原理知甲、乙均不与丙相邻有12+24=36,
故则甲、乙均不与丙相邻的概率$\frac{36}{120}$=$\frac{3}{10}$,
故答案为:$\frac{3}{10}$
点评 本题考查了排列和概率问题,站队问题是排列组合中的典型问题,解题时,要先排限制条件多的元素,本题解题的关键是看清题目的实质,把实际问题转化为数学问题,解出结果以后再还原为实际问题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{56}$ | B. | $\frac{9}{28}$ | C. | $\frac{9}{14}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [1,+∞) | C. | (-∞,1) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
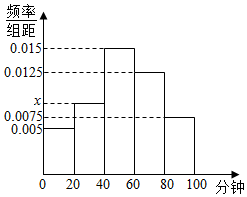 某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2$\sqrt{3}$-2 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恰有1件正品和恰有1件次品 | B. | 至少有1件次品和恰有1件次品 | ||
| C. | 至少有1件次品和至少有1件正品 | D. | 至少有1件正品和全部是次品 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com