
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得${e^{x_0}}≤0$ | |
| B. | $sinx+\frac{1}{sinx}≥2(x≠kπ,k∈Z)$ | |
| C. | ?x∈R,2x>x2 | |
| D. | 若命题p:?x0∈R,使得$x_0^2-{x_0}+1<0$,则¬p:?x0∈R,都有x2-x+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
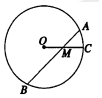 圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )
圆内两条相交弦长,其中一弦长为8cm,且被交点平分,另一条弦被交点分成1:4两部分,则这条弦长是( )| A. | 2cm | B. | 8cm | C. | 10cm | D. | 12cm |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,2] | B. | [-7,-6] | C. | [-9,-4] | D. | [-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为美化环境,某市计划在以A、B两地为直径的半圆弧$\widehat{AB}$上选择一点C建造垃圾处理厂(如图所示).已知A、B两地的距离为10km,垃圾场对某地的影响度与其到该地的距离关,对A、B两地的总影响度为对A地的影响度和对B地影响度的和.记C点到A地的距离为xkm,垃圾处理厂对A、B两地的总影响度为y.统计调查表明:垃圾处理厂对A地的影响度与其到A地距离的平方成反比,比例系数为$\frac{3}{2}$;对B地的影响度与其到B地的距离的平方成反比,比例系数为k.当垃圾处理厂建在弧$\widehat{AB}$的中点时,对A、B两地的总影响度为0.15.
为美化环境,某市计划在以A、B两地为直径的半圆弧$\widehat{AB}$上选择一点C建造垃圾处理厂(如图所示).已知A、B两地的距离为10km,垃圾场对某地的影响度与其到该地的距离关,对A、B两地的总影响度为对A地的影响度和对B地影响度的和.记C点到A地的距离为xkm,垃圾处理厂对A、B两地的总影响度为y.统计调查表明:垃圾处理厂对A地的影响度与其到A地距离的平方成反比,比例系数为$\frac{3}{2}$;对B地的影响度与其到B地的距离的平方成反比,比例系数为k.当垃圾处理厂建在弧$\widehat{AB}$的中点时,对A、B两地的总影响度为0.15.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com