
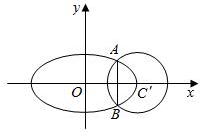
 ��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$����ԲC��ԲC�䣺��x-2��2+y2=1���ҽ���A��B�������㣬�ҽ��㶼��ԲC������ཻ���õ���AB��Ϊ$\frac{2\sqrt{5}}{3}$
��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$����ԲC��ԲC�䣺��x-2��2+y2=1���ҽ���A��B�������㣬�ҽ��㶼��ԲC������ཻ���õ���AB��Ϊ$\frac{2\sqrt{5}}{3}$���� ��1�����A��x0��y0������x0��0��y0��0��������֪�Ƶ���|C��E|=2-x0��x0�ʣ�1��2�������ҳ���ʽ����|AE|2+|C��E|2=|AC��|2���Ӷ�A��$\frac{4}{3}��\frac{\sqrt{5}}{3}$����������Բ������ԲC�������ʣ��������ԲC�ı����̣�
�������㣨1��0����ֱ��Ϊy=0ʱ��$\overrightarrow{OM}•\overrightarrow{ON}$=-4�������㣨1��0����ֱ�߲�Ϊy=0ʱ����Ϊx=ty������$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{x=ty+1}\end{array}\right.$���ã�t2+4��y2+2ty-3=0���ɸ���ϵ���Ĺ�ϵ����$\overrightarrow{OM}•\overrightarrow{ON}$=x1x2+y1y2=-4+$\frac{17}{{t}^{2}+4}$���ɡ���0��������ɴ������$\overrightarrow{OM}•\overrightarrow{ON}$�����ֵ��
��� �⣺��1����ͼ�����A��x0��y0������x0��0��y0��0��
����x��Ľ���ΪE����|C��E|=2-x0��
�߽��㶼��Բ��C�������x0�ʣ�1��2����
���ҳ���ʽ����|AE|2+|C��E|2=|AC��|2��
�ࣨ$\frac{\sqrt{5}}{3}$��2+��2-x0��2=12��
���${x}_{0}=\frac{8}{3}$���ᣩ����${x}_{0}=\frac{4}{3}$��
��${x}_{0}=\frac{4}{3}$����ԲC�䣺��x-2��2+y2=1�У����${y}_{0}=\frac{\sqrt{5}}{3}$����A��$\frac{4}{3}��\frac{\sqrt{5}}{3}$����
����A��$\frac{4}{3}$��$\frac{\sqrt{5}}{3}$��������ԲC��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����
��$\frac{16}{9{a}^{2}}+\frac{5}{9{b}^{2}}=1$����
����ԲC�İ뽹��Ϊc��������ԲC��������Ϊ$\frac{\sqrt{3}}{2}$����$\frac{c}{a}=\frac{\sqrt{3}}{2}$����
��a2=b2+c2����
�ɢ٢ڢۣ����a=2��b=1��c=$\sqrt{3}$��
����ԲC�ı�����Ϊ$\frac{{x}^{2}}{4}+{y}^{2}$=1��
�������㣨1��0����ֱ��Ϊy=0ʱ��$\overrightarrow{OM}•\overrightarrow{ON}$=��2��0��•��-2��0��=-4��
�����㣨1��0����ֱ�߲�Ϊy=0ʱ����Ϊx=ty��M��x1��y1����N��x2��y2����
����$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{x=ty+1}\end{array}\right.$�����ã�t2+4��y2+2ty-3=0��
�ɸ���ϵ���Ĺ�ϵ��${y}_{1}+{y}_{2}=-\frac{2t}{{t}^{2}+4}$��${y}_{1}{y}_{2}=-\frac{3}{{t}^{2}+4}$��
��$\overrightarrow{OM}•\overrightarrow{ON}$=x1x2+y1y2=��ty1+1����ty2+1��+y1y2
=��t2+1��y1y2+t��y1+y2��+1
=��t2+1��•$\frac{-3}{{t}^{2}+4}$+t•$\frac{-2t}{{t}^{2}+4}$+1
=$\frac{-4{t}^{2}+1}{{t}^{2}+4}$=$\frac{-4��{t}^{2}+4��+17}{{t}^{2}+4}$=-4+$\frac{17}{{t}^{2}+4}$��
���ɡ�=4t2+12��t2+4��=16t2+48��0���������t��R��
������ʽ����t=0ʱ����$\overrightarrow{OM}•\overrightarrow{ON}$��max=$\frac{1}{4}$��
��$\overrightarrow{OM}•\overrightarrow{ON}$�����ֵΪ$\frac{1}{4}$��
���� ���⿼����Բ���̵������������������������ֵ����ע���ҳ���ʽ������ϵ���Ĺ�ϵ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��0 | B�� | a+b+c��0 | C�� | b��0 | D�� | c��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{15}}}{4}$ | B�� | $\frac{{\sqrt{3}}}{2}$ | C�� | $\frac{{\sqrt{6}}}{5}$ | D�� | $\frac{{2\sqrt{2}}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com