
分析 根据两角和的正弦公式和二倍角的正余弦公式即可求得sin3x=4sinxcos2x-sinx,这样进行向量数量积的坐标运算便可得出f(x)=-4(sin2x-m)2+4m2,可看出0≤sin2x≤1,从而为求f(x)的最大值需讨论m,进而便可得出f(x)的最大值$g(m)=\left\{\begin{array}{l}{0}&{m<0}\\{4{m}^{2}}&{0≤m≤1}\\{8m-4}&{m>1}\end{array}\right.$,这样在g(m)的每段函数上解g(m)<5-|m-1|,所得m的范围再求并集即为原不等式的解集.
解答 解:f(x)=$\overrightarrow{a}•\overrightarrow{b}=sinxsin3x+(8m-3)si{n}^{2}x$
=sinx(sinxcos2x+cosxsin2x)+(8m-3)sin2x
=sinx(2sinxcos2x-sinx+2sinxcos2x)+(8m-3)sin2x
=4sin2xcos2x-4sin2x+8msin2x
=-4sin4x+8msin2x
=-4(sin2x-m)2+4m2;
∴0≤m≤1时,sin2x=m时,f(x)取最大值4m2;
m<0时,sin2x=0时,f(x)取最大值0;
m>1时,sin2x=1时,f(x)取最大值8m-4;
∴$g(m)=\left\{\begin{array}{l}{0}&{m<0}\\{4{m}^{2}}&{0≤m≤1}\\{8m-4}&{m>1}\end{array}\right.$;
∴①m<0时,由g(m)<5-|m-1|得,0<5-(1-m);
∴-4<m<0;
②0≤m≤1时,由g(m)<5-|m-1|得,4m2<5-(1-m);
解得$\frac{1-\sqrt{65}}{8}<m<\frac{1+\sqrt{65}}{8}$;
∴0≤m≤1;
③m>1时,由g(m)<5-|m-1|得,8m-4<5-(m-1);
∴$1<m<\frac{10}{9}$;
∴综上得,不等式g(m)<5-|m-1|的解集为$(-4,\frac{10}{9})$.
点评 考查两角和的正弦公式,以及二倍角的正余弦公式,sin2x+cos2x=1,配方法求二次式子的最大值,正弦函数的值域,对于分段函数g(m),解不等式g(m)<5-|m-1|的方法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
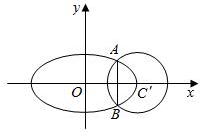 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,椭圆C与圆C′:(x-2)2+y2=1有且仅有A,B两个交点,且交点都在圆C′的左方,相交所得的弦AB长为$\frac{2\sqrt{5}}{3}$
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,椭圆C与圆C′:(x-2)2+y2=1有且仅有A,B两个交点,且交点都在圆C′的左方,相交所得的弦AB长为$\frac{2\sqrt{5}}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com