
分析 (1)由已知可得,点C的轨迹是以A为焦点,l1为准线的抛物线,由此能求出轨迹E的方程.
(2)设直线l2的方程为y=kx+1,与抛物线C方程联立消掉y得x的二次方程,设P(x1,y1),Q(x2,y2),易求R点坐标,由弦长公式及韦达定理把|PR|•|QR|表示出来,可得关于k的函数,由$α∈[{\frac{π}{6},\frac{π}{4}}]$,得k的范围,构造函数,根据函数的单调性即可求得|PR|•|QR|的最小值.
解答 解:(1)由已知可得,点C的轨迹是以A为焦点,l1为准线的抛物线,
∴轨迹E的方程为x2=4y.…(4分)
(2)设直线l2的方程为y=kx+1,代入抛物线方程x2=4y消去y,得x2-4kx-4=0.
记P(x1,y1),Q(x2,y2),则x1+x2=4k,x1x2=-4.
因为直线l2的斜率k≠O,易得点R的坐标为(-$\frac{2}{k}$,-1).
|AR|•|BR|=$\sqrt{1+{k}^{2}}$|x1-xR|•$\sqrt{1+{k}^{2}}$|x2-xR|
=(1+k2)•(x1+$\frac{2}{k}$)(x2+$\frac{2}{k}$)=(1+k2) x1 x2+($\frac{2}{k}$+2 k)( x1+x2)+$\frac{4}{{k}^{2}}$+4
=-4(1+k2)+4k($\frac{2}{k}$+2k)+$\frac{4}{{k}^{2}}$+4=4(k2+$\frac{1}{{k}^{2}}$)+8,
又$α∈[{\frac{π}{6},\frac{π}{4}}]$,∴k∈[$\frac{\sqrt{3}}{3}$,1],k2∈[$\frac{1}{3}$,1],
令t=k2,∵f(t)=4(t+$\frac{1}{t}$)+8在[$\frac{1}{3}$,1]上递减,
所以|PR|•|QR|的最小值为16.
点评 本题考查点的轨迹方程的求法,考查直线与圆锥曲线的综合应用,考查函数思想,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,$\frac{3}{2}$) | B. | [$\frac{\sqrt{2}}{2}$,$\frac{3}{2}$) | C. | [$\frac{\sqrt{2}}{4}$,1) | D. | [1,$\frac{3}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
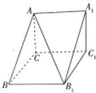 在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AB=2BC,AC=AA1=$\sqrt{3}$BC,则直线AB1与平面BB1C1C所成的角的正切值为( )
在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AB=2BC,AC=AA1=$\sqrt{3}$BC,则直线AB1与平面BB1C1C所成的角的正切值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{13}}{4}$ | D. | $\frac{\sqrt{39}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,12] | B. | (0,24] | C. | (0,36] | D. | (0,48] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (a-1)2(a+2) | B. | (a+1)2(a+2) | C. | (a-1)(a+1)(a-2) | D. | (a-1)2(a-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com