练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．与y=|x|为同一函数的是（　　）
    A．y=（$\sqrt{x}$）2B．y=a${\;}^{{{log}_a}x}}$C．y=$\left\{\begin{array}{l}x，（x＞0）\\-x，（x＜0）\end{array}$D．y=$\sqrt{x^2}$

    分析 根据y=$\sqrt{{x}^{2}}$=|x|，即可得出．

    解答 解：∵y=$\sqrt{{x}^{2}}$=|x|，
    ∴y=$\sqrt{{x}^{2}}$与y=|x|为同一函数，
    故选：D．

    点评 本题考查了根式的运算性质、函数的定义，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．已知f（x）=$\frac{1}{2}a{x^2}$-（2a+1）x+2lnx．
    （1）若曲线y=f（x）在x=1和x=3处的切线互相平行，求实数a的值；
    （2）求f（x）单调区间；
    （3）设g（x）=x2-2x，若对任意的x1∈（0，2]，存在x2∈[0，2]，使f（x1）＜g（x2），求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．设f（x）=$\frac{1}{{{4^x}+2}}$，利用课本中推导等差数列前n项和公式的方法，可求得f（$\frac{1}{10}$）+f（$\frac{2}{10}$）+…+f（$\frac{9}{10}$）=$\frac{9}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．直线y=2x的参数方程是（　　）
    A．$\left\{{\begin{array}{l}{x=\sqrt{t}}\\{y=2\sqrt{t}}\end{array}}\right.$B．$\left\{{\begin{array}{l}{x=2t+1}\\{y=4t+1}\end{array}}\right.$C．$\left\{{\begin{array}{l}{x=cosθ}\\{y=2sinθ}\end{array}}\right.$D．$\left\{{\begin{array}{l}{x=tanθ}\\{y=2tanθ}\end{array}}\right.$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

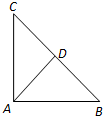    4．如图，已知△ABC中，AB=AC=4，∠BAC=$\frac{π}{2}$，点D是BC的中点，若向量$\overrightarrow{AM}$=$\frac{1}{4}$$\overrightarrow{AB}$+m$\overrightarrow{AC}$，且点M在△ACD的内部（不含边界），则$\overrightarrow{AM}•\overrightarrow{BM}$的取值范围是（　　）
    A．（-2，4）B．（-2，6）C．（0，4）D．（0，6）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．设f（x）=x2cosθ-x（1-x）+（1-x）2sinθ在x∈[0，1]时，f（x）＞0恒成立．
    （1）求证：sinθ＞0，cosθ＞0；          
    （2）求θ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．对于任意的实数a，b，c，下列命题正确的是（　　）
    A．若a＞b，c=0，则ac＞bcB．若ac2＞bc2，则a＞b
    C．若a＞b，则$\frac{1}{a}$＞$\frac{1}{b}$D．若a＞b，则ac2＞bc2
    E．若a＞b，则ac2＞bc2   

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．（1）函数f（x）=ax2+bx满足：1≤f（1）≤2，2≤f（-2）≤4，求f（-1）的取值范围．
    （2）若不等式ax2-ax+1≥0对x∈R恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知向量$\overrightarrow a$=（-1，-2），$\overrightarrow b$=（1，λ），若$\overrightarrow a$，$\overrightarrow b$的夹角为钝角，则λ的取值范围是（　　）
    A．（-∞，-$\frac{1}{2}$）B．（-$\frac{1}{2}$，2）∪（2，+∞）C．（-$\frac{1}{2}$，+∞）D．（2，+∞）

    查看答案和解析>>

    同步练习册答案