
分析 根据等比数列和等差数列的定义建立方程关系进行求解即可.
解答 解:设四个数分别为a-3d,a-d,a+d,a+3d,
把它们分别加上4,3,3,5之后为a-3d+4,a-d+3,a+d+3,a+3d+5,这四个数成等比数列,
则(a-d+3)2=(a-3d+4)(a+d+3)且(a+d+3)2=(a-d+3)(a+3d+5),
整理得4d2-2a+2d-6=0 ①
且4d2-a-d-3=0 ②,
②-①得a=3d-3,代入②得d2-d=0,
解得d=0,a=-3或d=1,a=0,
当d=0,a=-3时,四个数分别为0,0,0,0,把它们分别加上4,3,3,5之后为4,3,3,5不成等比数列,不满足条件.
当d=1,a=0,四个数分别为-3,-1,1,3,把它们分别加上4,3,3,5之后为1,2,4,8成等比数列,满足条件.
故四个数分别为-3,-1,1,3
点评 本题主要考查等比数列和等差数列的计算,根据条件建立方程关系是解决本题的关键.计算量比较大.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36种 | B. | 72种 | C. | 144种 | D. | 288种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
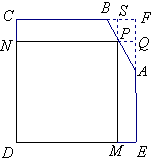 有一块铁皮零件,其形状是由边长为40cm的正方形截去一个三角形ABF所得的五边形ABCDE,其中AF=12cm,BF=10cm,如图所示.现在需要用这块材料截取矩形铁皮DMPN,使得矩形相邻两边分别落在CD,DE上,另一顶点P落在边CB或BA边上.设DM=xcm,矩形DMPN的面积为ycm2.
有一块铁皮零件,其形状是由边长为40cm的正方形截去一个三角形ABF所得的五边形ABCDE,其中AF=12cm,BF=10cm,如图所示.现在需要用这块材料截取矩形铁皮DMPN,使得矩形相邻两边分别落在CD,DE上,另一顶点P落在边CB或BA边上.设DM=xcm,矩形DMPN的面积为ycm2. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com