
【题目】在平面直角坐标系xOy中,曲线y=x2-6x+1与![]() 轴交于
轴交于![]() 点,与
点,与![]() 轴交于
轴交于![]() ,
, ![]() 两点.
两点.
(1)求△![]() 的面积;
的面积;
(2)求△![]() 外接圆的方程.
外接圆的方程.
科目:高中数学 来源: 题型:
【题目】如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(1)求AC的长;
(2)试比较BE与EF的长度关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,且
,且![]() .
.
(1)当![]() 时,写出
时,写出![]() 的通项公式(直接写出答案,无需过程);
的通项公式(直接写出答案,无需过程);
(2)求最小整数![]() ,使得当
,使得当![]() 时,
时, ![]() 是单调递增数列;
是单调递增数列;
(3)是否存在![]() 使得
使得![]() 是等比数列?若存在请求出;若不存在请说明理由.
是等比数列?若存在请求出;若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2015﹣2016赛季CBA联赛中,某队甲、乙两名球员在前10场比赛中投篮命中情况统计如下表(注:表中分数 ![]() ,N表示投篮次数,n表示命中次数),假设各场比赛相互独立.
,N表示投篮次数,n表示命中次数),假设各场比赛相互独立.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
根据统计表的信息:
(1)从上述比赛中等可能随机选择一场,求甲球员在该场比赛中投篮命中率大于0.5的概率;
(2)试估计甲、乙两名运动员在下一场比赛中恰有一人命中率超过0.5的概率;
(3)在接下来的3场比赛中,用X表示这3场比赛中乙球员命中率超过0.5的场次,试写出X的分布列,并求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形∠CAB=90°,AC=2a,E,F分别为AC,BC的中点,沿EF将△CEF折起,得到如图2所示的四棱锥C′﹣ABFE
(1)求证:AB⊥平面AEC′;
(2)当四棱锥C′﹣ABFE体积取最大值时,
①若G为BC′中点,求异面直线GF与AC′所成角;
②在C′﹣ABFE中AE交BF于C,求二面角A﹣CC′﹣B的余弦值.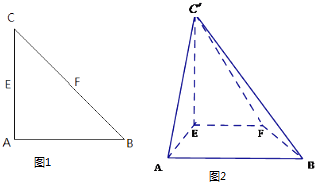
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
.
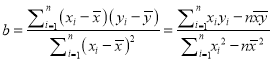 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2) ![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com