练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．设x∈R，定义符号函数sgnx=$\left\{\begin{array}{l}{1，x＞0}\\{0，x=0}\\{-1，x＜0}\end{array}\right.$，则（　　）
    A．|x|=x|sgnx|B．|x|=xsgn|x|C．|x|=|x|sgnxD．|x|=xsgnx

    分析 去掉绝对值符号，逐个比较即可．

    解答 解：对于选项A，右边=x|sgnx|=$\left\{\begin{array}{l}{x，}&{x≠0}\\{0，}&{x=0}\end{array}\right.$，而左边=|x|=$\left\{\begin{array}{l}{x，}&{x≥0}\\{-x，}&{x＜0}\end{array}\right.$，显然不正确；
    对于选项B，右边=xsgn|x|=$\left\{\begin{array}{l}{x，}&{x≠0}\\{0，}&{x=0}\end{array}\right.$，而左边=|x|=$\left\{\begin{array}{l}{x，}&{x≥0}\\{-x，}&{x＜0}\end{array}\right.$，显然不正确；
    对于选项C，右边=|x|sgnx=$\left\{\begin{array}{l}{x，}&{x≠0}\\{0，}&{x=0}\end{array}\right.$，而左边=|x|=$\left\{\begin{array}{l}{x，}&{x≥0}\\{-x，}&{x＜0}\end{array}\right.$，显然不正确；
    对于选项D，右边=xsgnx=$\left\{\begin{array}{l}{x，}&{x＞0}\\{0，}&{x=0}\\{-x，}&{x＜0}\end{array}\right.$，而左边=|x|=$\left\{\begin{array}{l}{x，}&{x≥0}\\{-x，}&{x＜0}\end{array}\right.$，显然正确；
    故选：D．

    点评 本题考查函数表达式的比较，正确去绝对值符号是解决本题的关键，注意解题方法的积累，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．已知数列{an}满足a1=$\frac{1}{2}$且an+1=an-an2（n∈N*）
    （1）证明：1＜$\frac{a_n}{{{a_{n+1}}}}$≤2（n∈N*）；
    （2）设数列{an2}的前n项和为Sn，证明$\frac{1}{2（n+2）}≤\frac{S_n}{n}≤\frac{1}{2（n+1）}$（n∈N*）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=ln$\frac{1+x}{1-x}$，
    （Ⅰ）求曲线y=f（x）在点（0，f（0））处的切线方程；
    （Ⅱ）求证，当x∈（0，1）时，f（x）＞$2（x+\frac{{x}^{3}}{3}）$；
    （Ⅲ）设实数k使得f（x）$＞k（x+\frac{{x}^{3}}{3}）$对x∈（0，1）恒成立，求k的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费xi和年销售量yi（i=1，2，…，8）数据作了初步处理，得到下面的散点图及一些统计量的值．

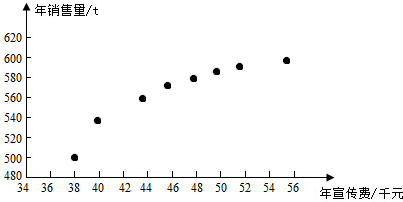
    $\overline{x}$$\overline{y}$$\overline{w}$$\sum _{i=1}^{8}$（xi-$\overline{x}$）2$\sum _{i=1}^{8}$（wi-$\overline{w}$）2$\sum _{i=1}^{8}$（xi-$\overline{x}$）（yi-$\overline{y}$）$\sum _{i=1}^{8}$（wi-$\overline{w}$）（yi-$\overline{y}$）
    46.65636.8289.81.61469108.8
    表中wi=$\sqrt{x}$i，$\overline{w}$=$\frac{1}{8}$$\sum _{i=1}^{8}w{\;}_{i}$
    （Ⅰ）根据散点图判断，y=a+bx与y=c+d$\sqrt{x}$哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）
    （Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；
    （Ⅲ）已知这种产品的年利润z与x、y的关系为z=0.2y-x．根据（Ⅱ）的结果回答下列问题：
    （i）年宣传费x=49时，年销售量及年利润的预报值是多少？
    （ii）年宣传费x为何值时，年利润的预报值最大？
    附：对于一组数据（u1 v1），（u2 v2）…..（un vn），其回归线v=α+βu的斜率和截距的最小二乘估计分别为：$\widehat{β}$=$\frac{\sum_{i=1}^{n}（{u}_{1}-\overline{u}）（{v}_{1}-\overline{v}）}{\sum_{i=1}^{n}（{u}_{1}-\overline{u}）^{2}}$，$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设函数f（x）=ex（2x-1）-ax+a，其中a＜1，若存在唯一的整数x0使得f（x0）＜0，则a的取值范围是（　　）
    A．[$-\frac{3}{2e}，1$）B．[$-\frac{3}{2e}，\frac{3}{4}$）C．[$\frac{3}{2e}，\frac{3}{4}$）D．[$\frac{3}{2e}，1$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．如图，已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形，AA1=6，且AA1⊥底面ABCD，点P、Q分别在棱DD1、BC上．
    （1）若P是DD1的中点，证明：AB1⊥PQ；
    （2）若PQ∥平面ABB1A1，二面角P-QD-A的余弦值为$\frac{3}{7}$，求四面体ADPQ的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知${\overrightarrow e_1}，{\overrightarrow e_2}$是空间单位向量，${\overrightarrow e_1}•{\overrightarrow e_2}=\frac{1}{2}$，若空间向量$\overrightarrow b$满足$\overrightarrow b•{\overrightarrow e_1}=2，\overrightarrow b•{\overrightarrow e_2}=\frac{5}{2}$，且对于任意x，y∈R，$|{\overrightarrow b-（x\overrightarrow{e_1}+y\overrightarrow{e_2}）}|≥|{\overrightarrow b-（{x_0}\overrightarrow{e_1}+{y_0}\overrightarrow{e_2}）}|$=1（x0，y0∈R），则x0=1，y0=2，$|{\overrightarrow b}$|=2$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=sin（${\frac{π}{2}$-x）sinx-$\sqrt{3}$cos2x．
    （I）求f（x）的最小正周期和最大值；
    （II）讨论f（x）在[${\frac{π}{6}$，$\frac{2π}{3}}$]上的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．如图，某港口一天6时到18时的水渠变化曲线近似满足函数y=3sin（$\frac{π}{6}$x+φ）+k．据此函数可知，这段时间水深（单位：m）的最大值为8．

    查看答案和解析>>

    同步练习册答案