
分析 (Ⅰ)$\overrightarrow{OM}$⊥x轴,可得M(0,1)或(0,-1),分别讨论M的坐标,求得直线MD方程,代入椭圆方程,解方程可得P的坐标;
(Ⅱ)设M(x1,y1),N(x2,y2),P(x3,y3),Q(x4,y4),可得直线MD的方程为x=$\frac{{x}_{1}-1}{{y}_{1}}$y+1,代入椭圆方程,运用韦达定理,可得P的坐标,同样可得Q的坐标,运用直线的斜率公式,可得k2,化简整理成k1的式子,即可得到证明.
解答 解:(Ⅰ)$\overrightarrow{OM}$⊥x轴,可得M(0,1)或(0,-1),
当M(0,1),D(1,0),可得直线MD的方程为x+y=1,
代入椭圆方程x2+9y2=9,可得10x2-18x=0,
解得x=0或x=$\frac{9}{5}$,
即有P($\frac{9}{5}$,-$\frac{4}{5}$);
当M(0,-1),可得直线MD的方程为y=x-1,
代入椭圆方程x2+9y2=9,可得10x2-18x=0,
解得x=0或x=$\frac{9}{5}$,
即有P($\frac{9}{5}$,$\frac{4}{5}$);
(Ⅱ)证明:设M(x1,y1),N(x2,y2),P(x3,y3),Q(x4,y4),
则直线MD的方程为x=$\frac{{x}_{1}-1}{{y}_{1}}$y+1,
代入椭圆方程整理得[9+($\frac{{x}_{1}-1}{{y}_{1}}$)2]y2+2y•$\frac{{x}_{1}-1}{{y}_{1}}$-8=0,
即有y1y3=-$\frac{8{{y}_{1}}^{2}}{9{{y}_{1}}^{2}+({x}_{1}-1)^{2}}$,
可得y3=-$\frac{8{y}_{1}}{9{{y}_{1}}^{2}+({x}_{1}-1)^{2}}$,
则x3=$\frac{-8({x}_{1}-1)+9{{y}_{1}}^{2}+({x}_{1}-1)^{2}}{9{{y}_{1}}^{2}+({x}_{1}-1)^{2}}$
由x12+9y12=9,即9y12=9-x12,
即有x3=$\frac{9-5{x}_{1}}{5-{x}_{1}}$,y3=-$\frac{4{y}_{1}}{5-{x}_{1}}$,
即P($\frac{9-5{x}_{1}}{5-{x}_{1}}$,-$\frac{4{y}_{1}}{5-{x}_{1}}$),
同理Q($\frac{9-5{x}_{2}}{5-{x}_{2}}$,-$\frac{4{y}_{2}}{5-{x}_{2}}$),
由M,A,N共线,
可得$\frac{{y}_{1}}{{x}_{1}+2}$=$\frac{{y}_{2}}{{x}_{2}+2}$=k1=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$,
又k2=$\frac{{y}_{4}-{y}_{3}}{{x}_{4}-{x}_{3}}$=$\frac{20({y}_{1}-{y}_{2})+4({x}_{1}{y}_{2}-{x}_{2}{y}_{1})}{16({x}_{1}-{x}_{2})}$
=$\frac{5{k}_{1}({x}_{1}-{x}_{2})+{x}_{1}{k}_{1}({x}_{2}+2)-{x}_{2}{k}_{1}({x}_{1}+2)}{4({x}_{1}-{x}_{2})}$
=$\frac{7{k}_{1}({x}_{1}-{x}_{2})}{4({x}_{1}-{x}_{2})}$=$\frac{7}{4}$k1,
则$\frac{{k}_{1}}{{k}_{2}}$=$\frac{4}{7}$.
点评 本题考查椭圆的方程和性质,注意联立直线方程和椭圆方程求交点,运用韦达定理和直线的斜率公式,考查化简整理的运算能力,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
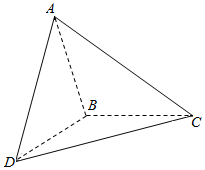 三棱锥A-BCD中,平面ABC⊥平面BCD,AB=BC=BD,∠ABC=∠DBC=120°,则二面角A-BD-C的平面角的正切值是-2.
三棱锥A-BCD中,平面ABC⊥平面BCD,AB=BC=BD,∠ABC=∠DBC=120°,则二面角A-BD-C的平面角的正切值是-2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cos2x | B. | y=2|sinx| | C. | y=($\frac{1}{3}$)cosx | D. | y=tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com