
分析 (1)根据新定义,从第一项一次往后写即可.
(2)结合第一归纳法,由猜想来验证即可.
解答 解:(1)由题意,易知(a1)n=a1=1
(a2)1=2a2-a1=9,(a2)1-1=8
(a2)2=2(a2)1-a1=17,(a2)1-1=16
(a2)3=2(a2)2-a1=33,(a2)2-1=32
(a2)4=2(a2)3-a1=65,(a2)2-1=64
(2)(an)1=nan-(n-1)an-1=8n-7,(n≥2)
∵(a1)1=1=8-7,∴(an)1=8n-7,(n∈N+)
(an)2=n(an)1-(n-1)(an-1)1=6n-15,(n≥2)
∵(a1)2=1=8-7,∴(an)2=16n-15,(n∈N+)
猜想(an)i=2i+2n-2i+2+1,(n∈N+)
当i=1时,(an)1=21+2n-21+2+1,(n∈N+)成立
假设当i=k时,(an)k=2k+2n-2k+2+1,(n∈N+)成立
则当i=k+1时
(an)k+1=n(an)k-(n-1)(an-1)k=n(2k+2n-2k+2+1)-(n-1)[2k+2(n-1)-2k+2+1]
=2k+2n2-(2k+2-1)n-2k+2(n-1)2+(2k+2-1)(n-1)
=2k+1+2n-2k+1+2+1(n≥2)
$({a}_{1})_{k+1}=1={2}^{k+1+2}-{2}^{k+1+2}+1$,即猜想成立,${(a}_{n})_{i}={2}^{i+2}n-{2}^{i+2}+1,(n∈{N}_{+})$
故对任意给定的m≥2且m∈N+,$({a}_{m})_{n}={2}^{n+2}m-{2}^{n+2}+1,(n∈{N}_{+})$
$({a}_{m})_{n}-1={2}^{n+2}m-{2}^{n+2}$=2n+2(m-1),(n∈N+)
所以$\frac{({a}_{m})_{n+1}-1}{({a}_{m})_{n}-1}$=$\frac{{2}^{n+3}(m-1)}{{2}^{n+2}(m-1)}=2,(n∈{N}_{+})$
即数列{(am)n-1}为公比为2的等比数列
点评 本题考查新定义,以及对第一归纳法的考查.解题的关键是对新定义的理解.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
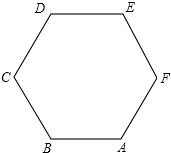
| A. | $\overrightarrow{CA}$+$\overrightarrow{CE}$=$\overrightarrow{CF}$ | B. | $\overrightarrow{CE}$-$\overrightarrow{AF}$=$\overrightarrow{AB}$ | C. | $\overrightarrow{BD}$•$\overrightarrow{FD}$=0 | D. | $\overrightarrow{CD}$•($\overrightarrow{AB}$-$\overrightarrow{AE}$-$\overrightarrow{EF}$)=-6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2) | B. | (-2,2) | C. | (-1,3) | D. | (-3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
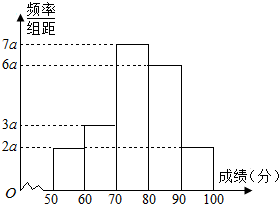 某班40名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.(学生成绩都在[50,100]之间)
某班40名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.(学生成绩都在[50,100]之间)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
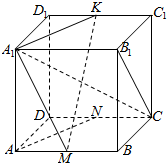 如图所示,M、N、K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点.求证:
如图所示,M、N、K分别是正方体ABCD-A1B1C1D1的棱AB,CD,C1D1的中点.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com