
分析 (Ⅰ)对任意的n∈N*,n≥2,由an+1=4an-3an-1,变形an+1-an=3an-3an-1=3(an-an-1),令bn=an+1-an,显然bn=an+1-an≠0,则$\frac{b_n}{{{b_{n-1}}}}=\frac{{{a_{n+1}}-{a_n}}}{{{a_n}-{a_{n-1}}}}=3$,即可证明.
(II)由(Ⅰ)可知${b_n}={b_1}×{q^{n-1}}={3^{n-1}}$.当n≥2时,${a_n}-{a_{n-1}}={b_{n-1}}={3^{n-2}}$,利用“累加求和”方法、“错位相减法”即可得出.
解答 (Ⅰ)证明:对任意的n∈N*,n≥2,∵an+1=4an-3an-1,
∴an+1-an=3an-3an-1=3(an-an-1),
令bn=an+1-an,显然bn=an+1-an≠0,则$\frac{b_n}{{{b_{n-1}}}}=\frac{{{a_{n+1}}-{a_n}}}{{{a_n}-{a_{n-1}}}}=3$,
∴数列{bn}是首项为b1=a2-a1=1,公比q为3的等比数列.
(Ⅱ)解:由(Ⅰ)可知${b_n}={b_1}×{q^{n-1}}={3^{n-1}}$.
∴当n=1时,a1=1,
当n≥2时,a2-a1=b1=1,${a_3}-{a_2}={b_2}={3^1}$,${a_3}-{a_2}={b_2}={3^2}$,…${a_n}-{a_{n-1}}={b_{n-1}}={3^{n-2}}$,
累加得${a_n}-{a_1}=1+{3^1}+{3^2}+…+{3^{n-2}}=\frac{{{3^{n-1}}-1}}{2}$${a_n}=1+\frac{{{3^{n-1}}-1}}{2}=\frac{{{3^{n-1}}+1}}{2}$,
∵${a_n}=\frac{{{3^{n-1}}+1}}{2}$,则$n•({{a_n}-\frac{1}{2}})=n•\frac{{{3^{n-1}}}}{2}$,
∴${S_n}=1×\frac{3^0}{2}+2×\frac{3^1}{2}+3×\frac{3^2}{2}+…+({n-1})×\frac{{{3^{n-2}}}}{2}+n×\frac{{{3^{n-1}}}}{2}$,
$3{S_n}=1×\frac{3^1}{2}+2×\frac{3^2}{2}+3×\frac{3^3}{2}+…+({n-1})×\frac{{{3^{n-1}}}}{2}+n×\frac{3^n}{2}$,
∴$-2{S_n}=\frac{3^0}{2}+\frac{3^1}{2}+\frac{3^2}{2}+…+\frac{{{3^{n-1}}}}{2}-n×\frac{3^n}{2}$=$\frac{{{3^n}-1}}{4}-n×\frac{3^n}{2}=\frac{{({1-2n}){3^n}-1}}{4}$,
∴${S_n}=\frac{{({2n-1}){3^n}+1}}{8}$.
点评 本题考查了递推关系、等比数列的通项公式与前n项和公式、“累加求和”方法、“错位相减法”,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
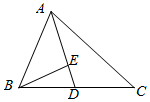 如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,AB=2,AC=3,D在线段BC上.
如图,在△ABC中,已知∠BAC=$\frac{π}{3}$,AB=2,AC=3,D在线段BC上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -20 | B. | -30 | C. | 15 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com