Question

20．已知动圆M过点F（0，$\frac{1}{4}$），且与直线4y+1=0相切．
（1）求点M的轨迹方程；
（2）求与直线2x+y-3=0平行且与M的轨迹相切的直线方程并求切点P的坐际；
（3）若直线1与点M的轨迹相切，l与直线4y+1=0相交于点A，与直线4y-1=0相交于点B，求证：△FAB是等腰三角形．

Answer 1

分析 （1）根据抛物线的定义即可求点M的轨迹方程；
（2）根据直线与抛物线的相切，利用削元法，转化为判别式△=0，即可得到结论．
（3）设出切线的切点坐标求出切线方程，求出A，B的坐标，计算|AF|=|BF|，即可得到结论．

解答 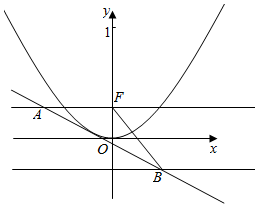解：（1）设动圆M的圆心M（x，y），半径R，
∵动圆M过点F（0，$\frac{1}{4}$），且与直线4y+1=0相切．
∴圆心到直线y=$-\frac{1}{4}$的距离d=R，MF=R，
则MF=d，
即M的轨迹是以F为焦点，y=$-\frac{1}{4}$为准线的抛物线，
则对应的抛物线方程为x²=y．
（2）设与直线2x+y-3=0平行的直线为2x+y+b=0
若2x+y+b=0与x²=y相切得x²=-2x-b，
即x²+2x+b=0，由判别式△=4-4b=0得b=1，此时切线方程为2x+y+1=0，
此时x=-$\frac{2}{2}$=-1，y=1，即切点P坐标为（-1，1）．
（3）设直线l与x²=y相切，切线为（m，m²），
则函数y=x²的导数f′（x）=2x，
则切线斜率k=2m，
则切线方程为y-m²=2m（x-m），
即y=2mx-m²，
当y=$\frac{1}{4}$，得x=$\frac{{m}^{2}+\frac{1}{4}}{2m}$，则A（$\frac{{m}^{2}+\frac{1}{4}}{2m}$，$\frac{1}{4}$），
当y=-$\frac{1}{4}$，得x=$\frac{{m}^{2}-\frac{1}{4}}{2m}$，则B（$\frac{{m}^{2}-\frac{1}{4}}{2m}$，-$\frac{1}{4}$），
则|AF|=|$\frac{{m}^{2}+\frac{1}{4}}{2m}$|，
|BF|=$\sqrt{（\frac{{m}^{2}-\frac{1}{4}}{2m}）^{2}+\frac{1}{4}}$=$\sqrt{（\frac{{m}^{2}+\frac{1}{4}}{2m}）^{2}}$=|$\frac{{m}^{2}+\frac{1}{4}}{2m}$|，
则|AF|=|BF|，
即：△FAB是等腰三角形．

点评 本题主要考查轨迹的计算，根据抛物线的定义求出抛物线的方程，以及利用直线和抛物线相切是解决本题的关键．