
| 3+x |
| 3-x |
| x |
| 3 |
| 3 |
| x |
| A、(-9,0)∪(0,9) |
| B、(-9,-1)∪(1,9) |
| C、(-3,-1)∪(1,3) |
| D、(-9,-3)∪(3,9) |
| 3+x |
| 3-x |
| x |
| 3 |
| 3 |
| x |
|
| 3+x |
| 3-x |
| 3+x |
| 3-x |
| x+3 |
| x-3 |
| x |
| 3 |
| 3 |
| x |
|
|


科目:高中数学 来源: 题型:
| a(x-1)(x-3) |
| A、-1 | B、-2 | C、-3 | D、-4 |
查看答案和解析>>
科目:高中数学 来源:[同步]人教B版选修4-5 1.1不等式的性质和一元二次不等式的解法(解析版) 题型:选择题
(2014•宝山区二模)在R上定义运算*:x*y=x•(1﹣y).若关于x的不等式x*(x﹣a)>0的解集是集合{x|﹣1≤x≤1}的子集,则实数a的取值范围是( )
A.[0,2] B.[﹣2,﹣1)∪(﹣1,0] C.[0,1)∪(1,2] D.[﹣2,0]
查看答案和解析>>
科目:高中数学 来源:[同步]人教B版选修4-5 1.1不等式的性质和一元二次不等式的解法(解析版) 题型:选择题
(2014•大庆二模)若a<b<0,则下列不等式不成立的是( )
A. >
>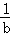 B.
B.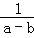 >
>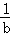 C.
C.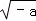 >
>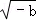 D.|a|>﹣b
D.|a|>﹣b
查看答案和解析>>
科目:高中数学 来源:[同步]2015年苏教版必修一 1.1 集合的含义及其表示练习卷(解析版) 题型:解答题
设集合A={2,3,a2+2a﹣3},集合B={|a+3|,2 },已知5∈A,且5∉B.求a的值.
查看答案和解析>>
科目:高中数学 来源:[同步]2015年北师大版必修二 2.3空间直角坐标系练习卷(解析版) 题型:选择题
点P(x,y,z)满足 =2,则点P在( )
=2,则点P在( )
A.以点(1,1,﹣1)为圆心,以2为半径的圆上
B.以点(1,1,﹣1)为中心,以2为棱长的正方体上
C.以点(1,1,﹣1)为球心,以2为半径的球面上
D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com