
| A. | 若平面α∥平面β,直线m∥平面α,则m∥β | |
| B. | 若平面α⊥平面γ,且平面β⊥平面γ,则α∥β | |
| C. | 平面α⊥平面β,其α∩β=l,点A∈α,A∉l,若直线AB⊥l,则AB⊥β | |
| D. | 直线m,n为异面直线,且m⊥平面α,n⊥平面β,若m⊥n,则α⊥β |
分析 根据平面与平面平行的性质进行判定,以及直线与平面位置关系的定义进行判定即可.
解答 解:因为平面α∥平面β,而直线m∥平面α
则当m在平面β内,原命题成立,
若m不在平面β内,则m一定与平面β平行;A错.
对于B,以正方体过同一顶点的三个面为例,确定其中一个面是β,另外两个面分别是α、γ,
可得α⊥β且β⊥γ,但α与γ不平行,因此B是假命题;
对于C,平面α⊥平面β,其α∩β=l,点A∈α,A∉l,若AB⊥l,则由平面与平面垂直的性质定理可知:AB⊥β,C正确.
对于D.直线m,n为异面直线,且m⊥平面α,n⊥平面β,若m⊥n,则α与β平行或相交.D错误.
故选:C
点评 本题主要考查了面面平行的性质,以及空间中直线与平面之间的位置关系,同时考查了空间想象能力,属于基础题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:选择题
| A. | l∥m且l⊥α | B. | l⊥m且l⊥α | C. | l⊥m且l∥α | D. | l∥m且l∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
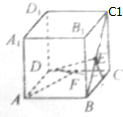 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BC1,DC的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BC1,DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com