解:(1)当b=1时f'(x)=3ax
2+2x-1,f(x)在(2,+∞)上存在单调递增区间,即f'(x)在(2,+∞)上存在区间使f'(x)>0.
①a>0时,f'(x)=3ax
2+2x-1是开口向上的抛物线.
显然f'(x)在(2,+∞)上存在区间,使f'(x)>0即a>0适合.
②a<0时,f'(x)=3ax
2+2x-1是开口向下的抛物线.
要使f'(x)在(2,+∞)上存在区间有f'(x)>0,则f'(x)=3ax
2+2x-1=0在(2,+∞)上有一解或两解.
即f'(2)>0或
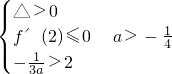
或无解,
又
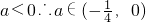
综合得
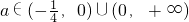
(2)不存在实数a,b,c满足条件.
事实上,由f(x
1)=f(x
2)得:a(x
13-x
23)+b(x
12-x
22)-(x
1-x
2)=0
∵x
1≠x
2∴a(x
12+x
1x
2+x
22)+b(x
1+x
2)-1=0
又f'(x)=3ax
2+2bx-1
∴
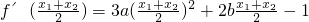
=

∵a≠0且
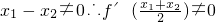
故不存在实数a,b,c满足条件.
分析:(1)首先由f(x)在(2,+∞)上存在单调递增区间,得(2,+∞)上存在区间使f'(x)>0;然后根据f'(x)=3ax
2+2x-1为二次函数,则对a进行分类讨论;特别是a<0时,有f'(x)=3ax
2+2x-1=0在(2,+∞)上有一解或两解两种情况;最后列出相应的不等式或不等式组解之即可.
(2)首先由f(x
1)=f(x
2)代入f(x)整理可得a(x
12+x
1x
2+x
22)+b(x
1+x
2)-1=0;再化简可得f′(

)=
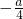
(x
1-x
2)
2≠0;最后判断出不存在这样的实数a,b,c满足条件.
点评:本题考查了函数单调性与其导数的关系,及导数的几何意义等基本知识;同时考查了学生分类讨论的思想方法与代数运算能力.

 处的切线斜率为0,若存在,求出一组实数a,b,c否则说明理由.
处的切线斜率为0,若存在,求出一组实数a,b,c否则说明理由.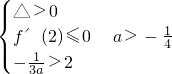 或无解,
或无解,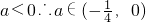
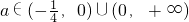
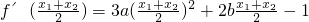

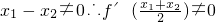
 )=
)=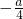 (x1-x2)2≠0;最后判断出不存在这样的实数a,b,c满足条件.
(x1-x2)2≠0;最后判断出不存在这样的实数a,b,c满足条件.
