
���� ������ԲC��Ϊ��ͨ���̵�$\frac{x^2}{4}+{y^2}=1$����$��=\frac{��}{3}$ʱ�����M��Ӧ�IJ���Ϊt0��ֱ��l���뷽��$\frac{{x}^{2}}{4}$+y2=1����$13{t^2}+4\sqrt{3}t-4=0$���ɴ��������M�����꣮
����$P��{\sqrt{3}��0}��$����l��$\left\{{\begin{array}{l}{x=\sqrt{3}+tcos��}\\{y=tsin��}\end{array}}\right.$���뷽��$\frac{x^2}{4}+{y^2}=1$����$��{{{cos}^2}��+4{{sin}^2}��}��{t^2}+��{2\sqrt{3}cos��}��t-1=0$���ɴ������ҳ���ʽ�����ֱ��l��б�ʣ�
��� �⣺������ԲC��$\left\{{\begin{array}{l}{x=2cos��}\\{y=sin��}\end{array}}\right.$��Ϊ��ͨ���̵�$\frac{x^2}{4}+{y^2}=1$��
��$��=\frac{��}{3}$ʱ�����M��Ӧ�IJ���Ϊt0��
ֱ��l�IJ�������Ϊ$\left\{{\begin{array}{l}{x=\sqrt{3}+\frac{1}{2}t}\\{y=\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$��tΪ��������
���뷽��$\frac{{x}^{2}}{4}$+y2=1�У���������$13{t^2}+4\sqrt{3}t-4=0$��
��ֱ��l�ϵĵ�A��B��Ӧ�IJ����ֱ�Ϊt1��t2��${t_1}+{t_2}=-\frac{{4\sqrt{3}}}{13}$��
��${t_0}=\frac{{{t_1}+{t_2}}}{2}=-\frac{{2\sqrt{3}}}{13}$��
���M������Ϊ$��{\frac{{12\sqrt{3}}}{13}��-\frac{3}{13}}��$��
����$P��{\sqrt{3}��0}��$����l��$\left\{{\begin{array}{l}{x=\sqrt{3}+tcos��}\\{y=tsin��}\end{array}}\right.$���뷽��$\frac{x^2}{4}+{y^2}=1$�У�
��$��{{{cos}^2}��+4{{sin}^2}��}��{t^2}+��{2\sqrt{3}cos��}��t-1=0$��
��${t_1}+{t_2}=-\frac{{2\sqrt{3}cos��}}{{{{cos}^2}��+4{{sin}^2}��}}$��${t_1}{t_2}=-\frac{1}{{{{cos}^2}��+4{{sin}^2}��}}$��
��|AB|=|t1|+|t2|=|t1-t2|=$\sqrt{��{t}_{1}+{t}_{2}��^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{��-\frac{2\sqrt{3}cos��}{co{s}^{2}��+4si{n}^{2}��}��^{2}+\frac{4}{co{s}^{2}��+4si{n}^{2}��}}$
=$\frac{4}{{{{cos}^2}��+4{{sin}^2}}}=\frac{4}{{1+3{{sin}^2}��}}$��
��$|{AB}|=\sqrt{3}|{OP}|$����$\frac{4}{{1+3{{sin}^2}��}}=3$��
${sin^2}��=\frac{1}{9}$��$sin��=\frac{1}{3}$��$cos��=��\frac{{2\sqrt{2}}}{3}$��
��ֱ��l��б��Ϊ$��\frac{{\sqrt{2}}}{4}$��
���� ���⿼���߶��е������������ֱ�ߵ�б�ʵ������е��⣬����ʱҪ�������⣬ע����Բ���������̡�ֱ�����ʵĺ������ã�


 ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{1��\frac{{\sqrt{5}}}{2}}��$ | B�� | $��{\sqrt{5}��+��}��$ | C�� | $��{\frac{{\sqrt{5}}}{2}��\sqrt{5}}��$ | D�� | $��{1��\frac{{\sqrt{5}}}{2}}���ȣ�{\sqrt{5}��+��}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
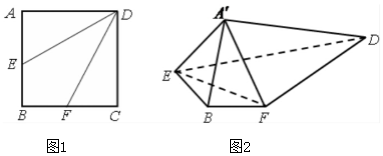 ��ͼ���߳�Ϊ2��������ABCD�У���E��AB���е㣬��F��BC���е㣮����AED����DCF�ֱ���DE��DF����ʹA��C�����غ��ڵ�A'������EF��A'B��
��ͼ���߳�Ϊ2��������ABCD�У���E��AB���е㣬��F��BC���е㣮����AED����DCF�ֱ���DE��DF����ʹA��C�����غ��ڵ�A'������EF��A'B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCDΪ���Σ�AB��CD��PD��ƽ��ABCD����BAD=��ADC=90�㣬$DC=2AB=2��DA=\sqrt{3}$��
��ͼ���ı���ABCDΪ���Σ�AB��CD��PD��ƽ��ABCD����BAD=��ADC=90�㣬$DC=2AB=2��DA=\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��Բ��x+2��2+y2=4��Բ��Ϊ��B��A��2��0����P��Բ������һ�㣬�߶�AP�Ĵ�ֱƽ����l��ֱ��BP�ཻ�ڵ�Q������P��Բ���˶�ʱ����Q�Ĺ켣����Ϊ${x^2}-\frac{y^2}{3}=1$��
��ͼ��Բ��x+2��2+y2=4��Բ��Ϊ��B��A��2��0����P��Բ������һ�㣬�߶�AP�Ĵ�ֱƽ����l��ֱ��BP�ཻ�ڵ�Q������P��Բ���˶�ʱ����Q�Ĺ켣����Ϊ${x^2}-\frac{y^2}{3}=1$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com