
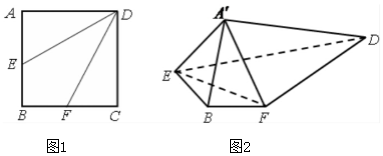
 如图,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点.将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A',连结EF,A'B.
如图,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点.将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A',连结EF,A'B.分析 (1)在正方形ABCD中,有AD⊥AE,CD⊥CF,可得A'D⊥A'E,A'D⊥A'F,由线面垂直的判定可得A'D⊥平面A'EF.从而得到A'D⊥EF;
(2)已知正方形ABCD的边长为2,点E是AB的中点,点F是BC的中点,可得A'E2+A'F2=EF2,则A'E⊥A'F,求出三角形A′EF的面积,结合(1)可知三棱锥D-A'EF的高A'D=2,代入棱锥体积公式求得三棱锥D-A'EF的体积.
解答 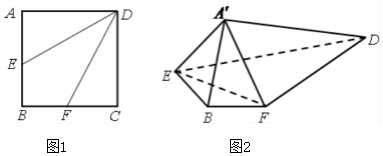 解:(1)在正方形ABCD中,
解:(1)在正方形ABCD中,
∵AD⊥AE,CD⊥CF,∴A'D⊥A'E,A'D⊥A'F,
又A'E∩A'F=A',A'E,A'F?平面A'EF,∴A'D⊥平面A'EF.
而EF?平面A'EF,∴A'D⊥EF,
∴异面直线A'D与EF所成角的大小为90°;
(2)∵正方形ABCD的边长为2,点E是AB的中点,点F是BC的中点,
∴在Rt△BEF中,BE=BF=1,得$EF=\sqrt{2}$,
而A'E=A'F=1,
∴A'E2+A'F2=EF2,则A'E⊥A'F,
∴${S_△}_{A'EF}=\frac{1}{2}×1×1=\frac{1}{2}$,
由(1)得A'D⊥平面A'EF,且A'D=2,
∴${V_{D-A'EF}}=\frac{1}{3}{S_{△A'EF}}A'D=\frac{1}{3}×\frac{1}{2}×2=\frac{1}{3}$.
点评 本题考查平面与平面平行的判定,考查空间想象能力和思维能力,训练了多面体体积的求法,属中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x>0,|x|>1 | B. | ?x>0,|x|≥1 | C. | ?x≤0,|x|<1 | D. | ?x≤0,|x|≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{2}{3},0]$ | B. | $[0,\frac{4}{3}]$ | C. | $[\frac{4}{3},2]$ | D. | [2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在直线y=-3x上 | B. | 在直线y=3x上 | C. | 在直线y=-4x上 | D. | 在直线y=4x上 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2=-4(y-1)(0<y≤1) | B. | x2=4(y-1)(0<y≤1) | C. | x2=4(y+1)(0<y≤1) | D. | x2=-2(y-1)(0<y≤1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com