
| A. | $[-\frac{2}{3},0]$ | B. | $[0,\frac{4}{3}]$ | C. | $[\frac{4}{3},2]$ | D. | [2,4] |
分析 根据题意求出t≥$\frac{{2cos}^{2}β}{2-cosβ}$,设f(t)=$\frac{{2cos}^{2}β}{2-cosβ}$,求出f(t)的最小值;再根据题意求出t≤$\frac{{4cos}^{2}β}{2-cosβ}$,设g(t)=$\frac{{4cos}^{2}β}{2-cosβ}$=2f(t),求出g(t)的最大值,从而求出实数t的取值范围.
解答 解:∵β∈[$\frac{π}{2}$,π],∴-1≤cosβ≤0;
∵α≤t,∴$t={cos^2}β+\frac{α}{2}cosβ$≥cos2β+$\frac{t}{2}$cosβ,
即t≥$\frac{{2cos}^{2}β}{2-cosβ}$;
令f(t)=$\frac{{2cos}^{2}β}{2-cosβ}$,则
f′(t)=$\frac{4cosβ•(-sinβ)(2-cosβ)-{2cos}^{2}βsinβ}{{(2-cosβ)}^{2}}$=$\frac{2cosβsinβ(cosβ-4)}{{(2-cosβ)}^{2}}$;
令f′(t)=0,解得sinβ=0或cosβ=0;
当sinβ=0时,cosβ=-1,
此时f(t)=$\frac{2}{2-(-1)}$=$\frac{2}{3}$,
当cosβ=0时,f(t)=0为最小值;
又t≤α-2cosβ,∴α≥t+2cosβ,
∴t≤cos2β+$\frac{t+2cosβ}{2}$•cosβ,
即t≤$\frac{{4cos}^{2}β}{2-cosβ}$;
令g(t)=$\frac{{4cos}^{2}β}{2-cosβ}$=2f(t),
则g′(t)=2f′(t)=2•$\frac{2cosβsinβ(cosβ-4)}{{(2-cosβ)}^{2}}$;
令g′(t)=0,解得sinβ=0或cosβ=0;
当sinβ=0时,cosβ=-1,
此时g(t)=2×$\frac{2}{3}$=$\frac{4}{3}$为最大值,
当cosβ=0时,g(t)=0;
综上,实数t的取值范围是[0,$\frac{4}{3}$].
故选:B.
点评 本题考查了三角函数的恒等变换应用以及导数的综合运用问题,也考查了构造函数与求最值问题,是综合性题目.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
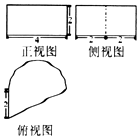 已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )
已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )| A. | 4π+8 | B. | 4π+12 | C. | 8π+8 | D. | 8π+12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
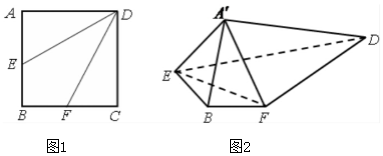 如图,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点.将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A',连结EF,A'B.
如图,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点.将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A',连结EF,A'B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (18,17,-17) | B. | (-14,-19,17) | C. | $({6,\frac{7}{2},1})$ | D. | $({-2,-\frac{11}{2},13})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com