
分析 从导数作为切入点探求函数的单调性,通过函数单调性来求得函数的值域,利用复合函数的求导公式进行求导,然后逐步分析即可
解答 解:(1)证明:f(x)=$\frac{x-2}{x+2}{e}^{x}$
f'(x)=ex($\frac{x-2}{x+2}+\frac{4}{(x+2)^{2}}$)=$\frac{{x}^{2}{e}^{x}}{(x+2)^{2}}$
∵当x∈(-∞,-2)∪(-2,+∞)时,f'(x)>0
∴f(x)在(-∞,-2)和(-2,+∞)上单调递增
∴x>0时,$\frac{x-2}{x+2}{e}^{x}$>f(0)=-1
即(x-2)ex+x+2>0
(2)g'(x)=$\frac{({e}^{x}-a){x}^{2}-2x({e}^{x}-ax-a)}{{x}^{4}}$
=$\frac{x(x{e}^{x}-2{e}^{x}+ax+2a)}{{x}^{4}}$=$\frac{(x+2)(\frac{x-2}{x+2}•{e}^{x}+a)}{{x}^{3}}$
a∈[0,1)
由(1)知,当x>0时,f(x)=$\frac{x-2}{x+2}{e}^{x}$的值域为(-1,+∞),只有一解使得
$\frac{t-2}{t+2}•{e}^{t}=-a$,
只需$\frac{t-2}{t+2}$•et≤0恒成立,可得-2<t≤2,
由x>0,可得
t∈(0,2]
当x∈(0,t)时,g'(x)<0,g(x)单调减;
当x∈(t,+∞),g'(x)>0,g(x)单调增;
h(a)=$\frac{{e}^{t}-a(t+1)}{{t}^{2}}$=$\frac{{e}^{t}+(t+1)\frac{t-2}{t+2}•{e}^{t}}{{t}^{2}}$=$\frac{{e}^{t}}{t+2}$
记k(t)=$\frac{{e}^{t}}{t+2}$,在t∈(0,2]时,k'(t)=$\frac{{e}^{t}(t+1)}{(t+2)^{2}}$>0,
故k(t)单调递增,
所以h(a)=k(t)∈($\frac{1}{2}$,$\frac{{e}^{2}}{4}$].
点评 该题考查了导数在函数单调性上的应用,重点是掌握复合函数的求导,以及导数代表的意义,计算量较大,难度较大.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:选择题
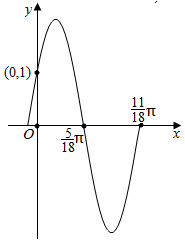
| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
| 出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 频数 | 60 | 50 | 30 | 30 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 1 | C. | 0 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com