
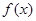 对任意的实数
对任意的实数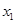 ,
,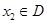 ,均有
,均有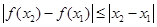 ,则称函数
,则称函数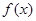 是区间
是区间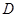 上的“平缓函数”.
上的“平缓函数”. 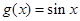 和
和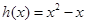 是不是实数集R上的“平缓函数”,并说明理由;
是不是实数集R上的“平缓函数”,并说明理由;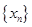 对所有的正整数
对所有的正整数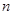 都有
都有 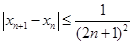 ,设
,设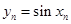 ,
, 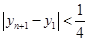 .
.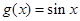 是R上的“平缓函数”,但
是R上的“平缓函数”,但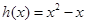 不是区间R的“平缓函数”;
不是区间R的“平缓函数”;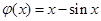 ,则
,则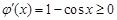 ,则
,则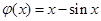 是实数集R上的增函数,
是实数集R上的增函数,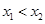 ,则
,则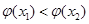 ,即
,即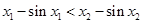 ,
, 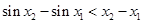 . ① …………… 1分
. ① …………… 1分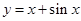 也是R上的增函数,则
也是R上的增函数,则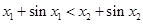 ,
,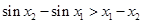 , ② ………… 2分
, ② ………… 2分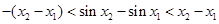 .
. 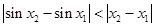 ,对
,对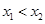 都成立. ……… 3分
都成立. ……… 3分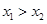 时,同理有
时,同理有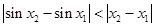 成立
成立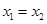 时,不等式
时,不等式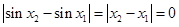 ,
,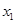 ,
,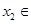 R,均有
R,均有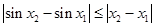 .
.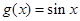 是R上的“平缓函数”. ………… 5分
是R上的“平缓函数”. ………… 5分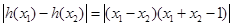 ………… 6分
………… 6分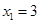 ,
,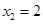 ,则
,则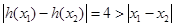 , ………… 7分
, ………… 7分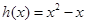 不是区间R的“平缓函数”. ………… 8分
不是区间R的“平缓函数”. ………… 8分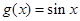 是R上的“平缓函数”,
是R上的“平缓函数”,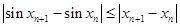 , 所以
, 所以 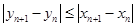 . …………… 9分
. …………… 9分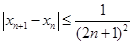 ,
,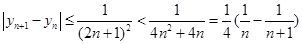 . …………… 10分
. …………… 10分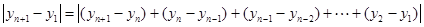 ,……… 11分
,……… 11分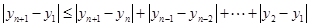 . …………… 12分
. …………… 12分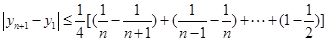
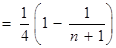 ………… 13分
………… 13分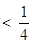 . ………… 14分
. ………… 14分

科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
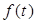 (元)与时间
(元)与时间 (天)的函数关系近似满足
(天)的函数关系近似满足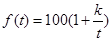 (
(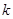 为正的常数),日销售量
为正的常数),日销售量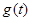 (件)与时间
(件)与时间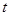 (天)的函数关系近似满足
(天)的函数关系近似满足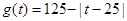 ,且第25天的销售金额为13000元.
,且第25天的销售金额为13000元.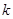 的值;
的值;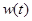 关于时间
关于时间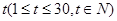 的函数关系式,并求前半个月销售金额
的函数关系式,并求前半个月销售金额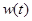 的最小值。
的最小值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com