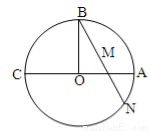
如图，AC为⊙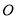
的直径，
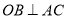,弦BN交AC于点M，若
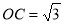，OM=1,则MN的长为 ．
轻巧夺冠周测月考直通中考系列答案科目：高中数学 来源：2015届湖南省高二下学期学业水平模拟考试数学试卷（解析版） 题型：解答题
已知
是首项
的递增等差数列，
为其前
项和，且
．
（1）求数列的通项公式；
（2）设数列
满足
，
为数列的前n项和．若对任意的
，不等式
恒成立，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源：2015届湖南省益阳市高三第一次模拟考试文科数学试卷（解析版） 题型：解答题
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下，大桥上的车流速度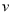
(单位：千米
/小时)是车流密度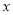
（单位：辆/千米）的函数.当桥上的的车流密度达到200辆/千米时，造成堵塞，此时车
流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时，研究表明，当
时，
车流速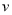度
是车流密度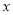的一次函数.
（1）当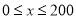
时，求函数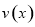
的表达式.
（2）当车流密度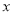
为多大时，车流量（单位时间内通过桥上某观点的车辆数，单位：辆/每小时）
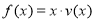可以达到最大，并求最大值（精确到1辆/每小时）.
查看答案和解析>>
科目：高中数学 来源：2015届湖南省益阳市高三第一次模拟考试文科数学试卷（解析版） 题型：选择题
“
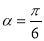”是“
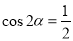”的（ ）
A．充分而不必要条件 B．必要而不充分条
C．充分必要条件 D．既不充分也不必要条件
查看答案和解析>>
科目：高中数学 来源：2015届湖南省高二下学期期末考试理科数学试卷（解析版） 题型：解答题
某中学在运动会期间举行定点投篮比赛，规定每人投篮4次，投中一球得2分，没有投中得0分，假设每次投篮投中与否是相互独立的，已知小明每次投篮投中的概率都是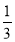
．
（1）求小明在投篮过程中直到第三次才投中的概率；
（2）求小明在4次投篮后的总得分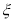
的分布列和期望．
查看答案和解析>>
科目：高中数学 来源：2015届湖南省高二下学期期末考试文科数学试卷（解析版） 题型：解答题
已知圆C过点P（1，1），且与圆M：(x+2)2+(x+2)2=r2(r>0)2关于直线x+y+2=0对称．
⑴求圆C的方程；
⑵设Q为圆C上的一个动点，求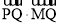
的最小值；
⑶过点P作两条相异直线分别与圆C相交于A，B，且直线PA和直线PB的倾斜角互补，O为坐标原点，试判断直线OP和AB是否平行？请说明理由．
查看答案和解析>>
科目：高中数学 来源：2015届湖北省高二下学期期中考试文科数学试卷（解析版） 题型：选择题
以抛物线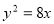
上的任意一点为圆心作圆与直线
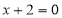相切，这些圆必过一定点，则这一定点的坐标是（ ）
A．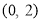
B．（2，0） C．（4，0） D．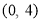
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，又因为OM=1，在
中由构股定理得：
，
,由相交弦定理知:
,
,故应填入:1．
的最小值是 （ ）
B、4 C、
D、5
，若
，则a=
B、
C、1 D、2