
分析 利用正弦定理求得和已知等式分别求得b和c,b和a的关系,最后利用余弦定理求得cosA的值,求得A,则tanA可求得.
解答 解:∵sinC=2$\sqrt{3}$sinB,
∴c=2$\sqrt{3}$b,
∴$\frac{a}{b}=\frac{b+\sqrt{3}c}{a}$=$\frac{b+6b}{a}$,
∴a2=7b2,
cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{{b}^{2}+12{b}^{2}-7{b}^{2}}{4\sqrt{3}{b}^{2}}$=$\frac{\sqrt{3}}{2}$,
∴A=$\frac{π}{6}$,
∴tanA=$\frac{\sqrt{3}}{3}$,
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题主要考查了正弦定理和余弦定理的运用.正弦定理和余弦定理是解三角形问题常用公式,应能熟练和灵活运用.


科目:高中数学 来源: 题型:选择题
| A. | 0.15 | B. | 0.25 | C. | 0.2 | D. | 0.18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
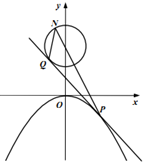 如图,曲线C1:x2=-4y,曲线C2:x2+(y-m)2=1(m>0),过曲线C1上的一点P(2,-1)作曲线C1的切线l,且l与C2恰好相切,切点为Q.
如图,曲线C1:x2=-4y,曲线C2:x2+(y-m)2=1(m>0),过曲线C1上的一点P(2,-1)作曲线C1的切线l,且l与C2恰好相切,切点为Q.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 95% | B. | 99% | C. | 97.5% | D. | 90% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{e}$ | B. | -$\frac{1}{e}$ | C. | e | D. | -e |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | af(b)>bf(a) | B. | af(a)>bf(b) | C. | bf(a)>af(b) | D. | bf(b)>af(a) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 2 | 3 | 10 | 15 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | x | 3 | 1 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 9 | 8 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 3 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com