
分析 (Ⅰ)记“从盒中随机抽取一个零件,抽到的是使用过零件”为事件A.可得P(A)=$\frac{{∁}_{2}^{1}}{{∁}_{7}^{1}}$.利用二项分布列可得:三次抽取中恰有2次抽到使用过零件的概率P=${∁}_{3}^{2}(\frac{2}{7})^{2}(\frac{5}{7})$.
(II)利用二项分布列的计算公式即可得出.
解答 解:(Ⅰ)记“从盒中随机抽取一个零件,抽到的是使用过零件”为事件A.
则P(A)=$\frac{{∁}_{2}^{1}}{{∁}_{7}^{1}}$=$\frac{2}{7}$.
所以三次抽取中恰有2次抽到使用过零件的概率P=${∁}_{3}^{2}(\frac{2}{7})^{2}(\frac{5}{7})$=$\frac{60}{343}$.
(Ⅱ)从盒中任意抽取三个零件,使用后放回盒子中,设此时盒子中使用过的零件个数为X,
由已知X=3,4,5.
P(X=3)=$\frac{{∁}_{5}^{1}{∁}_{2}^{2}}{{∁}_{7}^{3}}$=$\frac{1}{7}$,P(X=4)=$\frac{{∁}_{5}^{2}{∁}_{2}^{1}}{{∁}_{7}^{3}}$=$\frac{4}{7}$,P(X=5)=$\frac{{∁}_{5}^{3}}{{∁}_{7}^{3}}$=$\frac{2}{7}$.
随机变量X的分布列为:
| X | 3 | 4 | 5 |
| P | $\frac{1}{7}$ | $\frac{4}{7}$ | $\frac{2}{7}$ |
点评 本题考查了二项分布列与超几何分布列的概率计算公式及其数学期望,考查了推理能力与计算能力,属于中档题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4.5 | C. | 3.5 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
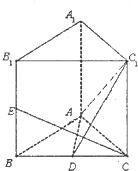 如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.
如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
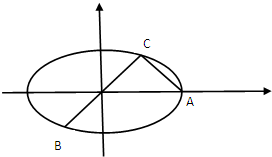 如图,已知A,B,C是长轴为4的椭圆E上的三点,点A是长轴的
如图,已知A,B,C是长轴为4的椭圆E上的三点,点A是长轴的查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{14}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com