
分析 可作出图形,根据向量加法的平行四边形法则及加法的几何意义即可判断①②的正误,对于③④,可以根据条件得到$x\overrightarrow{OA}+\overrightarrow{OM}=\frac{1}{2x}\overrightarrow{BO}$,然后根据向量加法的平行四边形法及平行线分线段成比例定理便可得到$1-\frac{1}{-2x}=-\frac{x}{2}$,可解出x=-1,这样即可判断结论④正确.
解答 解:如图,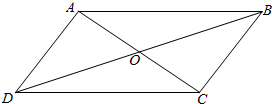
①$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}=2\overrightarrow{AO}$,该结论正确;
②$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}$=$(\overrightarrow{MO}+\overrightarrow{OA})+(\overrightarrow{MO}+\overrightarrow{OB})$$+(\overrightarrow{MO}+\overrightarrow{OC})+(\overrightarrow{MO}+\overrightarrow{OD})$=$4\overrightarrow{MO}+(\overrightarrow{OA}+\overrightarrow{OC})+(\overrightarrow{OB}+\overrightarrow{OD})$=$4\overrightarrow{MO}$,∴该结论错误;
③根据条件知,x≠0,∴$\frac{x}{2}\overrightarrow{OA}+\overrightarrow{OB}=\frac{1}{2x}\overrightarrow{BO}$,x<0,如图,作MN∥AC,NE∥OM,分别交OB于N,OC于E;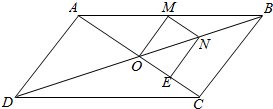
则$ON=\frac{1}{-2x}OB$,$OE=MN=-\frac{x}{2}AO$;
∴$1-\frac{1}{-2x}=-\frac{x}{2}$;
∴解得x=-1;
∴$MN=\frac{1}{2}AO$;
∴M为AB的中点;
∴③错误,④正确;
∴正确的结论为①④.
故答案为:①④.
点评 考查向量加法的平行四边形法则,向量加法的几何意义,以及共线向量基本定理,平行线分线段成比例定理.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{81}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{9}$ | D. | $\frac{8}{81}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com