
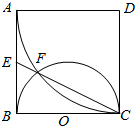
 如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.
如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.分析 (1)推导出EA为圆D的切线,且EB是圆O的切线,由此利用切割线定理能证明AE=EB.
(2)在Rt△BCE中,由射影定理得BE2=EF•EC,即可得到要求的线段.
解答 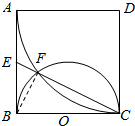 (1)证明:由以D为圆心DA为半径作圆,而ABCD为正方形,
(1)证明:由以D为圆心DA为半径作圆,而ABCD为正方形,
∴EA为圆D的切线
依据切割线定理得EA2=EF•EC…(2分)
∵圆O以BC为直径,∴EB是圆O的切线,
同样依据切割线定理得EB2=EF•EC…(2分)
故AE=EB…(5分)
所以点E为AB的中点
(2)解:连结BF,∵BC为圆O的直径,∴BF⊥EC
又在Rt△BCE中,由射影定理得BE2=EF•EC
所以$EF=\frac{{B{E^2}}}{EC}=\frac{1}{{\sqrt{5}}}=\frac{{\sqrt{5}}}{5}$…(10分)
点评 本题考查切割线定理,考查射影定理,是一个中档题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{2}+\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{3}+2\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{2}+2\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{2}+\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 图象关于(π,0)中心对称 | B. | 图象关于直线x=$\frac{π}{2}$对称 | ||
| C. | g(x)是周期为π的奇函数 | D. | 在区间[-$\frac{π}{6}$,0]上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 不充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com