
| A. | 图象关于(π,0)中心对称 | B. | 图象关于直线x=$\frac{π}{2}$对称 | ||
| C. | g(x)是周期为π的奇函数 | D. | 在区间[-$\frac{π}{6}$,0]上单调递增 |
分析 由二阶行列式展开式求出f(x)=2sin(2x+$\frac{π}{6}$),从而由平移性质得g(x)=-2cos2x,由此能求出结果.
解答 解:∵f(x)=$|\begin{array}{l}{co{s}^{2}x-si{n}^{2}x}&{\sqrt{3}}\\{cos(\frac{π}{2}+2x)}&{1}\end{array}|$
=cos2x-sin2x-$\sqrt{3}cos(\frac{π}{2}+2x)$
=cos2x+$\sqrt{3}sin2x$=2sin(2x+$\frac{π}{6}$),
f(x)的图象向右平移$\frac{π}{3}$个单位得到函数g(x),
∴g(x)=2sin(2x-$\frac{π}{2}$)=-2cos2x,
∴图象关于(π,0)中心对称为($\frac{kπ}{2}+\frac{π}{4}$,0),k∈Z,故A错误;
图象关于直线x=$\frac{kπ}{2}$,k∈Z对称,故B正确;
g(x)是周期为π的偶函数,故C错误;
函数在区间[-$\frac{π}{6}$,0]上单调递减,故D错误.
故选:B.
点评 本题考查命题真假的判断,是中档题,涉及到二阶行列式、三角函数性质、平移等知识的综合运用.


科目:高中数学 来源: 题型:解答题
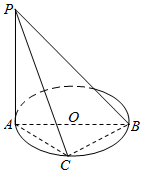 如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面ABC
如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面ABC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
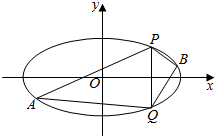 已知中心在原点,焦点在x轴上的椭圆C的离心率为$\frac{\sqrt{3}}{2}$,点(0,$\sqrt{2}$)是椭圆与y轴的一个交点.
已知中心在原点,焦点在x轴上的椭圆C的离心率为$\frac{\sqrt{3}}{2}$,点(0,$\sqrt{2}$)是椭圆与y轴的一个交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
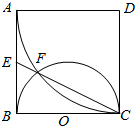 如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.
如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∉R,log2x=2015 | B. | ?x∈R,log2x≠2015 | ||
| C. | ?x0∈R,log2x0=2015 | D. | ?x0∈R,log2x0≠2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3α+β=\frac{π}{2}$ | B. | $2α+β=\frac{π}{2}$ | C. | $3α-β=\frac{π}{2}$ | D. | $2α-β=\frac{π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com