练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．已知命题p：?x∈R，log2x=2015，则￢p为（　　）
    A．?x∉R，log2x=2015B．?x∈R，log2x≠2015
    C．?x0∈R，log2x0=2015D．?x0∈R，log2x0≠2015

    分析 根据全称命题的否定是特称命题进行判断即可．

    解答 解：命题是全称命题，则命题的否定是特称命题，
    即?x0∈R，log2x0≠2015，
    故选：D．

    点评 本题主要考查含有量词的命题的否定，根据全称命题的否定是特称命题是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

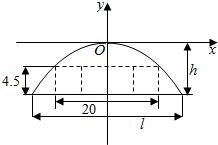    19．某隧道设计为双向四车道，车道总宽20米，要求通行车辆限高4.5米，隧道口截面的拱线近似地看成抛物线形状的一部分，如图所示建立平面直角坐标系xOy．
    （1）若最大拱高h为6米，则隧道设计的拱宽l是多少？
    （2）为了使施工的土方工程量最小，需隧道口截面面积最小．现隧道口的最大拱高h不小于6米，则应如何设计拱高h和拱宽l，使得隧道口截面面积最小？（隧道口截面面积公式为S=$\frac{2}{3}$lh）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．定义2×2矩阵$|\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}|$=a1a4-a2a3，若f（x）=$|\begin{array}{l}{co{s}^{2}x-si{n}^{2}x}&{\sqrt{3}}\\{cos（\frac{π}{2}+2x）}&{1}\end{array}|$，则f（x）的图象向右平移$\frac{π}{3}$个单位得到函数g（x），则函数g（x）的解析式为（　　）
    A．图象关于（π，0）中心对称B．图象关于直线x=$\frac{π}{2}$对称
    C．g（x）是周期为π的奇函数D．在区间[-$\frac{π}{6}$，0]上单调递增

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．“点P的轨迹方程为y=|x|”是“点P到两条坐标轴距离相等”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．不充分不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．一座抛物线形拱桥，高水位时，拱顶离水面3m，水面宽2$\sqrt{6}$m，当水面上升1m后，水面宽4m．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

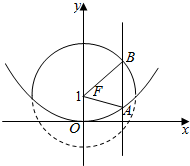    14．如图，直线x=m与抛物线x2=4y交于点A，与圆（y-1）2+x2=4的实线部分（即在抛物线开口内的圆弧）交于点B，F为抛物线的焦点，则△ABF的周长的取值范围是（　　）
    A．（2，4）B．（4，6）C．[2，4]D．[4，6]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）．
    （1）有一枚质地均匀的正四面体玩具，玩具的各个面上分别写着数字1，2，3，4．若先后两次投掷玩具，将朝下的面上的数字依次记为a，b，求双曲线C的离心率小于$\sqrt{5}$的概率；
    （2）在区间[1，6]内取两个数依次记为a，b，求双曲线C的离心率小于$\sqrt{5}$的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．一个盒子中装有2个红球和2个白球，这4个球除颜色外完全相同．
    （1）无放回的从中任取2次，每次取1个，取出的2个都是红球的概率；
    （2）有放回的从中任取2次，每次取1个，取出的2个都是红球的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若x，y满足不等式组$\left\{\begin{array}{l}x+2y-2≥0\\ x-y+1≥0\\ 2x+y-4≤0\end{array}\right.$，z=x-2y，则z的最大值是2．

    查看答案和解析>>

    同步练习册答案