
分析 先建立平面直角坐标系,抛物线方程假设为:x2=-2py(p>0),再利用当拱顶离水面3米,水面宽2$\sqrt{6}$米,求出抛物线方程,进而可求水面上升1m后,水面宽度.
解答 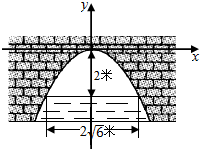 解:建立如图所示的平面直角坐标系,则抛物线方程可假设为:x2=-2py(p>0),
解:建立如图所示的平面直角坐标系,则抛物线方程可假设为:x2=-2py(p>0),
∵当拱顶离水面3米,水面宽2$\sqrt{6}$米,
∴($\sqrt{6}$,-3)代入抛物线方程可得:6=6p,
∴2p=2,
∴抛物线方程为:x2=-2y.
如果水面上升1m,则令y=-2,
∴x=±2,
∴水面宽4m,
故答案为:4.
点评 本题考查抛物线的应用,考查待定系数法求抛物线的方程,解题的关键是正确建立平面直角坐标系.


科目:高中数学 来源: 题型:解答题
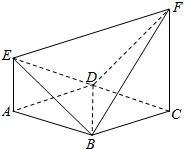 如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC∥EA,设EA=1
如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC∥EA,设EA=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
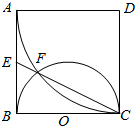 如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.
如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p1,p3 | B. | p1,p4 | C. | p2,p3 | D. | p2,p4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∉R,log2x=2015 | B. | ?x∈R,log2x≠2015 | ||
| C. | ?x0∈R,log2x0=2015 | D. | ?x0∈R,log2x0≠2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 2 | 3 | 5 | 6 |
| y | 7 | 8-a | 9+a | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q | B. | (¬p)∧(¬q) | C. | p∨(¬q) | D. | p∧q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com