
分析 运用作差比较法,结合分解因式和不等式的性质,即可得证.
解答 证明:由a,b,c为正数,
2($\frac{{a}^{2}}{b+c}$+$\frac{{b}^{2}}{c+a}$+$\frac{{c}^{2}}{a+b}$)-$\frac{{b}^{2}+{c}^{2}}{b+c}$-$\frac{{c}^{2}+{a}^{2}}{c+a}$-$\frac{{a}^{2}+{b}^{2}}{a+b}$
=$\frac{({a}^{2}-{b}^{2})+({a}^{2}-{c}^{2})}{b+c}$+$\frac{({b}^{2}-{c}^{2})+({b}^{2}-{a}^{2})}{c+a}$+$\frac{({c}^{2}-{a}^{2})+({c}^{2}-{b}^{2})}{a+b}$
=(a2-b2)($\frac{1}{b+c}$-$\frac{1}{c+a}$)+(b2-c2)($\frac{1}{c+a}$-$\frac{1}{a+b}$)+(c2-a2)($\frac{1}{a+b}$-$\frac{1}{b+c}$)
=$\frac{(a-b)^{2}(a+b)}{(b+c)(c+a)}$+$\frac{(b-c)^{2}(b+c)}{(a+b)(c+a)}$+$\frac{(c-a)^{2}(c+a)}{(a+b)(b+c)}$≥0,
当且仅当a=b=c时取得等号.
故原不等式成立.
点评 本题考查不等式的证明,注意运用作差比较法,结合因式分解,考查化简整理的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
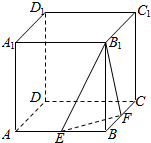 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{2}+\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{3}+2\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{2}+2\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{2}+\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
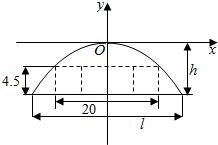 某隧道设计为双向四车道,车道总宽20米,要求通行车辆限高4.5米,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系xOy.
某隧道设计为双向四车道,车道总宽20米,要求通行车辆限高4.5米,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系xOy.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,PD=AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,PD=AD=1,PD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 图象关于(π,0)中心对称 | B. | 图象关于直线x=$\frac{π}{2}$对称 | ||
| C. | g(x)是周期为π的奇函数 | D. | 在区间[-$\frac{π}{6}$,0]上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com