
���� ��1������Բ�������ʵõ�a��b�Ĺ�ϵ������$\overrightarrow{PA}$•$\overrightarrow{PB}$����СֵΪ-2���a��ֵ����b������Բ���̿���
��2���ɣ�1��֪F1��-$\sqrt{2}$��0����F2��$\sqrt{2}$��0������б�ʲ�����ʱ��������ֱ��ʾ��$\overrightarrow{{F}_{2}M}$��$\overrightarrow{{F}_{2}N}$�ģ�ֱ�����$\overrightarrow{{F}_{2}M}$•$\overrightarrow{{F}_{2}N}$��ֱ��б�ʴ���ʱ����ֱ��MN�ķ���Ϊy=k��x+$\sqrt{2}$����������Բ����$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$����ȥy�ã�1+2k2��x2+4$\sqrt{2}$k2x+4��k2-1��=0�����ø���ϵ���Ĺ�ϵ���M��N�ĺ�������Ļ�����$\overrightarrow{{F}_{2}M}$•$\overrightarrow{{F}_{2}N}$ת��ΪM��N�ĺ�����ĺ��������ʽ�������Ϊ����k�ĺ���ʽ�ô𰸣�
��� �⣺��1��������֪��$\frac{c}{a}=\frac{\sqrt{2}}{2}$����$\frac{{c}^{2}}{{a}^{2}}=\frac{1}{2}$��
��$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{1}{2}$����a2=2b2��
��P��x��y����
��$\overrightarrow{PA}$•$\overrightarrow{PB}$=��-a-x��-y��•��a-x��-y��=x2-a2+y2=${x}^{2}-{a}^{2}+\frac{{a}^{2}}{2}-\frac{{x}^{2}}{2}=\frac{1}{2}��{x}^{2}-{a}^{2}��$��
��-a��x��a���൱x=0ʱ��$��\overrightarrow{PA}•\overrightarrow{PB}��_{min}=-\frac{{a}^{2}}{2}=-2$��
��a2=4����b2=2��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$��
��2����a2=4��b2=2����c=$\sqrt{{a}^{2}-{b}^{2}}=\sqrt{2}$��
��${F}_{1}��-\sqrt{2}��0����{F}_{2}��\sqrt{2}��0��$��
��ֱ��б�ʲ�����ʱ��
M��-$\sqrt{2}$��1����N��-$\sqrt{2}$��-1��������$\overrightarrow{{F}_{2}M}$=��-2$\sqrt{2}$��1����$\overrightarrow{{F}_{2}N}$=��-2$\sqrt{2}$��-1����
��$\overrightarrow{{F}_{2}M}$•$\overrightarrow{{F}_{2}N}$=7��
ֱ��б�ʴ���ʱ����ֱ��MN�ķ���Ϊy=k��x+$\sqrt{2}$����������Բ����$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$����ȥy��
��1+2k2��x2+4$\sqrt{2}$k2x+4��k2-1��=0��
��M��x1��y1����N��x2��y2����
��${x}_{1}+{x}_{2}=-\frac{4\sqrt{2}{k}^{2}}{1+2{k}^{2}}��{x}_{1}{x}_{2}=\frac{4��{k}^{2}-1��}{1+2{k}^{2}}$��
��$\overrightarrow{{F}_{2}M}=��{x}_{1}-\sqrt{2}��{y}_{1}����\overrightarrow{{F}_{2}N}=��{x}_{2}-\sqrt{2}��{y}_{2}��$��
��$\overrightarrow{{F}_{2}M}$•$\overrightarrow{{F}_{2}N}$=${x}_{1}{x}_{2}-\sqrt{2}��{x}_{1}+{x}_{2}��+2+{k}^{2}��{x}_{1}+\sqrt{2}����{x}_{2}+\sqrt{2}��$
=$��1+{k}^{2}��{x}_{1}{x}_{2}+��\sqrt{2}{k}^{2}-\sqrt{2}����{x}_{1}+{x}_{2}��$+2k2+2
=$��1+{k}^{2}��\frac{4��{k}^{2}-1��}{1+2{k}^{2}}+\sqrt{2}��{k}^{2}-1��•\frac{-4\sqrt{2}{k}^{2}}{1+2{k}^{2}}+2{k}^{2}+2$
=7-$\frac{9}{1+2{k}^{2}}$��
��1+2k2��1����0��$\frac{1}{1+2{k}^{2}}$��1��
��7-$\frac{9}{1+2{k}^{2}}$��[-2��7����
����֪��$\overrightarrow{{F}_{2}M}$•$\overrightarrow{{F}_{2}N}$��[-2��7]��
���� ����������Ϊ���壬������Բ�ı����̣�������������������������������������ʱӦע��������ۣ�ͬʱ��ȷ�������ʾ���������е���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
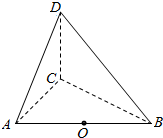 ��ͼ��ʾ������D-ABC�У�AC��BC��CD������ֱ��AC=CD=1��$BC=\sqrt{3}$����OΪAB�е㣮
��ͼ��ʾ������D-ABC�У�AC��BC��CD������ֱ��AC=CD=1��$BC=\sqrt{3}$����OΪAB�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
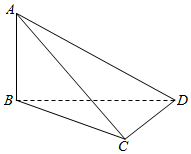 ��ͼ����������ABCD�У�AB��BD��CD��DB����AB��CD���ɵĽǵĴ�СΪ60�㣬������C-BD-A�Ĵ�СΪ��������
��ͼ����������ABCD�У�AB��BD��CD��DB����AB��CD���ɵĽǵĴ�СΪ60�㣬������C-BD-A�Ĵ�СΪ��������| A�� | 60���90�� | B�� | 60�� | C�� | 60���120�� | D�� | 30���150�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
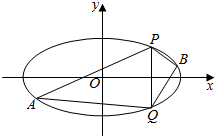 ��֪������ԭ�㣬������x���ϵ���ԲC��������Ϊ$\frac{\sqrt{3}}{2}$���㣨0��$\sqrt{2}$������Բ��y���һ�����㣮
��֪������ԭ�㣬������x���ϵ���ԲC��������Ϊ$\frac{\sqrt{3}}{2}$���㣨0��$\sqrt{2}$������Բ��y���һ�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ƽ��$\frac{��}{6}$����λ | B�� | ����ƽ��$\frac{��}{2}$����λ | ||
| C�� | ����ƽ��$\frac{��}{6}$����λ | D�� | ����ƽ��$\frac{��}{2}$����λ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com