
分析 作出平面图形,然后找出二面角的平面角,通过三角形的解法求解AB.
解答 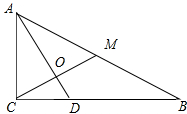
 解:△ABC中,∠C=$\frac{π}{2}$,∠B=$\frac{π}{6}$,AC=2,M是AB的中点,三角形ACM是正三角形,
解:△ABC中,∠C=$\frac{π}{2}$,∠B=$\frac{π}{6}$,AC=2,M是AB的中点,三角形ACM是正三角形,
取CM的中点为:O,连结AO并延长交CB于D,可知AO⊥CM,OD⊥CM,
则AC=AM=CM=MB=2,CO=OM=1,CB=2$\sqrt{3}$,AO=$\sqrt{3}$,CD=$\frac{2\sqrt{3}}{3}$,OD=$\frac{\sqrt{3}}{3}$,
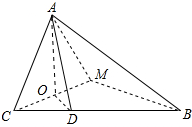
沿直线CM将CBM折起,在折叠后的图形中,
∵AO⊥CM,OD⊥CM,
∴∠AOD就是二面角B-CM-A的平面角,可知α=$\frac{π}{3}$.
∴AD=$\sqrt{3+\frac{1}{3}-2×\sqrt{3}×\frac{\sqrt{3}}{3}×\frac{1}{2}}$=$\sqrt{\frac{7}{3}}$
∴cos∠ACD=$\frac{4+\frac{4}{3}-\frac{7}{3}}{2×2×\frac{2\sqrt{3}}{3}}$=$\frac{3\sqrt{3}}{8}$
∴AB=$\sqrt{4+12-2×2×2\sqrt{3}×\frac{3\sqrt{3}}{8}}$=$\sqrt{7}$,
故答案为:$\sqrt{7}$.
点评 本题考查二面角的平面角的求法,考查空间想象能力以及转化思想的应用,考查计算能力.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:选择题
| A. | x+2y-2=0 | B. | x-2y+2=0 | C. | 2x-y+1=0 | D. | 2x-y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | (-∞,3] | C. | [3,+∞) | D. | [3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
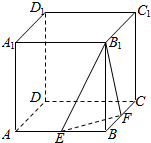 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com