
分析 (1)通过令分母不为0即得f(x)的定义域,通过求导即得f(x)的单调区间;
(2)通过(1)知x=r是f(x)的极大值点,计算即可.
解答 解:(1)∵函数f(x)=$\frac{ax}{{{{(x+r)}^2}}}$(a>0,r>0),
∴x≠-r,即f(x)的定义域为(-∞,-r)∪(-r,+∞).
又∵f(x)=$\frac{ax}{{{{(x+r)}^2}}}$=$\frac{ax}{{x}^{2}+2rx+{r}^{2}}$,
∴f′(x)=$\frac{a({x}^{2}+2rx+{r}^{2})-ax(2x+2r)}{({x}^{2}+2rx+{r}^{2})^{2}}$=$\frac{a(r-x)(x+r)}{(x+r)^{4}}$,
∴当x<-r或x>r时,f′(x)<0;当-r<x<r时,f′(x)>0;
因此,f(x)的单调递减区间为:(-∞,-r)、(r,+∞),递增区间为:(-r,r);
(2)由(1)的解答可得f′(x)=0,f(x)在(0,r)上单调递增,在(r,+∞)上单调递减,
∴x=r是f(x)的极大值点,
∴f(x)在(0,+∞)内的极大值为f(r)=$\frac{ar}{(2r)^{2}}$=$\frac{a}{4r}$=$\frac{400}{4}$=100.
点评 本题考查函数的定义域、单调区间、极值,注意解题方法的积累,属于中档题.


 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:解答题
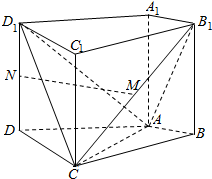 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$,且点M和N分别为B1C和D1D的中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$,且点M和N分别为B1C和D1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

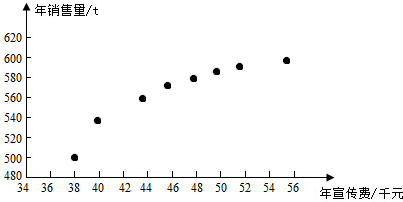
| A. | 逐年比较,2008年减少二氧化硫排放量的效果最显著 | |
| B. | 2007年我国治理二氧化硫排放显现成效 | |
| C. | 2006年以来我国二氧化硫年排放量呈减少趋势 | |
| D. | 2006年以来我国二氧化硫年排放量与年份正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum _{i=1}^{8}$(xi-$\overline{x}$)2 | $\sum _{i=1}^{8}$(wi-$\overline{w}$)2 | $\sum _{i=1}^{8}$(xi-$\overline{x}$)(yi-$\overline{y}$) | $\sum _{i=1}^{8}$(wi-$\overline{w}$)(yi-$\overline{y}$) |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$-\frac{3}{2e},1$) | B. | [$-\frac{3}{2e},\frac{3}{4}$) | C. | [$\frac{3}{2e},\frac{3}{4}$) | D. | [$\frac{3}{2e},1$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
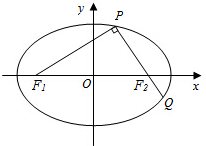 如题图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,且过F2的直线交椭圆于P,Q两点,且PQ⊥PF1.
如题图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,且过F2的直线交椭圆于P,Q两点,且PQ⊥PF1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com