
| A. | a>b>c | B. | a<b<c | C. | c>a>b | D. | b>a>c |
分析 根据a>b?a-b>0,因此要比较a,b的大小,作差,通分,利用对数的运算性质,即可求得a,b的大小;利用对数函数y=lnx的单调性,可知ln2π>ln6>0,然后利用不等式的可乘性,即可得出a,c的大小.
解答 解:a-b=$\frac{l{n}^{2}6}{4}$-ln2ln3=$\frac{(ln2+ln3)^{2}-4ln2ln3}{4}$=$\frac{{(ln2-ln3)}^{2}}{4}$>0,
∴a>b
而ln2π>ln6>0,
∴$\frac{l{n}^{2}2π}{4}$>$\frac{l{n}^{2}6}{4}$,
即c>a,
因此c>a>b,
故选C.
点评 本题考查不等式比较大小,其中作差法是常用方法,以及对数的运算性质和对数函数的单调性的考查,熟练掌握基础知识是解题的关键,属中档题.


科目:高中数学 来源: 题型:选择题
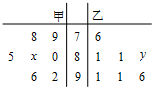 某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )
某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )| A. | 8 | B. | 7 | C. | 9 | D. | 168 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若ξ-B(4,0.25),则Eξ=1 | |
| B. | 命题“?x∈R,x2≥0”的否定是“?x0∈R,x02<0” | |
| C. | 从匀速传递的产品生产线上,检查人员每隔5分钟从中抽出一件产品检查,这样的抽样是系统抽样 | |
| D. | 10名工人某天生产同一零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,这组数据的中位数与众数相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| M | 900 | 700 | 300 | 100 |
| y | 0.5 | 3.5 | 6.5 | 9.5 |
| M | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
| 频数 | 3 | 6 | 12 | 6 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2kπ,2kπ+π)k∈Z | B. | (2kπ,2kπ+2π)k∈Z | C. | (kπ,kπ+$\frac{π}{2}$)k∈Z | D. | (kπ+$\frac{π}{2}$,kπ+π)k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com