
| A. | 若ξ-B(4,0.25),则Eξ=1 | |
| B. | 命题“?x∈R,x2≥0”的否定是“?x0∈R,x02<0” | |
| C. | 从匀速传递的产品生产线上,检查人员每隔5分钟从中抽出一件产品检查,这样的抽样是系统抽样 | |
| D. | 10名工人某天生产同一零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,这组数据的中位数与众数相等 |
分析 根据统计和命题的相关知识,逐一分析给定四个答案的真假,可得答案.
解答 解:A中,若ξ-B(4,0.25),则Eξ=4×0.25=1”,故正确;
B中,命题“?x∈R,x2≥0”的否定是“?x0∈R,x02<0”,故正确;
从匀速传递的产品生产线上,检查人员每隔5分钟从中抽出一件产品检查,这样的抽样是系统抽样,故正确;
10名工人某天生产同一零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,这组数据的中位数为15,众数为17,两者不等,故错误,
故选:D
点评 本题以命题的真假判断为载体,考查了二项分布,全称(特称)命题的判定,抽样方法,中位数与众数等知识点,难度不大,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
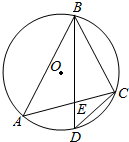 如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.
如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1+\frac{ln2}{2}$ | B. | $1-\frac{ln2}{2}$ | C. | $2\sqrt{e}-1$ | D. | $\sqrt{e}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a<b<c | C. | c>a>b | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com