
分析 (Ⅰ)枚举法列出所有满足条件的数对(x1,y1)即可,
(Ⅱ)由10000×$\frac{1}{{2}^{i}}$≤1250,得i≥3,由(Ⅰ)每轮过关的概率为$\frac{2}{9}$.某人闯关获得奖金不超过1250元的概率:P(i≥3)=1-P(i=1)-P(i=2)
(Ⅲ)设游戏第k轮后终止的概率为pk(k=1,2,3,4),分别求出相应的概率,由能求出X的分布列和数学期望.
解答 解:(Ⅰ),当y1=6时,x1<$\frac{36}{12}=3$,因此x1=1,2;
当y1=5时,x1<$\frac{30}{11}$,因此x1=1,2;
当y1=4时,x1<$\frac{24}{10}$,因此x1=1,2;
当y1=3时,x1<$\frac{18}{9}=2$,因此x1=1;
当y1=2时,x1<$\frac{12}{8}=\frac{3}{2}$因此x1=1;
当y1=1时,x1<$\frac{6}{7}$,因此x1无值;
∴第一轮闯关成功的概率P(A)=$\frac{8}{6×6}=\frac{2}{9}$.
(Ⅱ)令金数f(i)=10000×$\frac{1}{{2}^{i}}$≤1250,则i≥3,
由(Ⅰ)每轮过关的概率为$\frac{2}{9}$.
某人闯关获得奖金不超过1250元的概率
:P(i≥3)=1-P(i=1)-P(i=2)=1-$\frac{2}{9}$-(1-$\frac{2}{9}$)×$\frac{2}{9}$=$\frac{49}{81}$
(Ⅲ)依题意X的可能取值为1,2,3,4
设游戏第k轮后终止的概率为pk(k=1,2,3,4)
p1=$\frac{2}{9}$.p2=(1-$\frac{2}{9}$)×$\frac{2}{9}$=$\frac{14}{81}$,p3=(1-$\frac{2}{9}$)2×$\frac{2}{9}$=$\frac{98}{729}$,p4=1-p1-p2-p3=$\frac{343}{729}$;
故X的分布列为
| X | 1 | 2 | 3 | 4 |
| P | $\frac{2}{9}$ | $\frac{14}{81}$ | $\frac{98}{729}$ | $\frac{343}{729}$ |
点评 题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,独立重复试验的概率求解,是中档题,


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$-1 | D. | 2$\sqrt{2}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,-2) | B. | [-3,-2] | C. | (-∞,-3)∪(-2,+∞) | D. | (-∞,-3)∪[-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
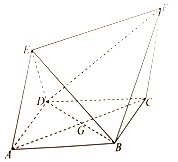 如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.
如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
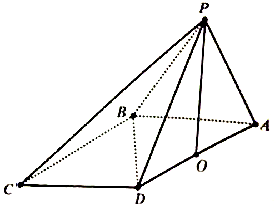 在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.
在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
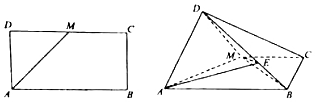
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
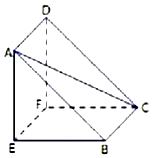 如图所示为一名曰“堑堵”的几何体,已知AE⊥底面BCFE,DF∥AE,DF=AE=1,CE=$\sqrt{7}$,四边形ABCD是正方形.
如图所示为一名曰“堑堵”的几何体,已知AE⊥底面BCFE,DF∥AE,DF=AE=1,CE=$\sqrt{7}$,四边形ABCD是正方形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com