
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 对于①:假设函数f(x)是“海宝”函数:则f(x)=x2≤$\frac{k}{2015}$|x|,x=0时,k∈R,x≠0时,化为k≥2015|x|,因此不存在k>0,使得x≠0成立,即可判断出结论;
同理可得②④也不是“海宝”函数.
对于③:假设函数f(x)是“海宝”函数:则|f(x)|=|$\frac{x}{{x}^{2}+x+1}$|≤$\frac{k}{2015}$|x|,x≤0时,成立;当x>0时,化为$\frac{1}{(x+\frac{1}{2})^{2}+\frac{3}{4}}$≤$\frac{k}{2015}$,可得:k≥$\frac{8060}{3}$,即可判断出结论.
解答 解:对于①:假设函数f(x)是“海宝”函数:则f(x)=x2≤$\frac{k}{2015}$|x|,x=0时,k∈R,x≠0时,化为k≥2015|x|,因此不存在k>0,使得x≠0成立,因此假设不正确,即函数f(x)不是“海宝”函数;
同理可得②④也不是“海宝”函数.
对于③:假设函数f(x)是“海宝”函数:则|f(x)|=|$\frac{x}{{x}^{2}+x+1}$|≤$\frac{k}{2015}$|x|,x≤0时,只要取:k≥$\frac{8060}{3}$,成立;当x>0时,化为$\frac{1}{(x+\frac{1}{2})^{2}+\frac{3}{4}}$≤$\frac{k}{2015}$,
可得:k≥$\frac{8060}{3}$,因此只要取:k≥$\frac{8060}{3}$,则函数f(x)=$\frac{x}{{x}^{2}+x+1}$是“海宝”函数.
故选:A.
点评 本题考查了新定义“海宝”函数、分类讨论方法、函数的单调性及其最值,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1} | C. | [-2,0] | D. | {-2,-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
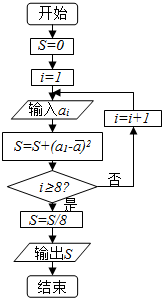 对一名学生数学成绩统计了8次,第i次统计得到的数据为ai,具体如下表所示:
对一名学生数学成绩统计了8次,第i次统计得到的数据为ai,具体如下表所示:| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ai | 100 | 101 | 103 | 103 | 104 | 106 | 107 | 108 |
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
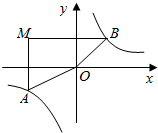 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.
如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com