
| A. | y=2x+1 | B. | y=log3(x-2) | C. | y=$\frac{2}{x}$ | D. | y=cosx |
分析 根据题意,得出函数y=f(x)图象上任一点M(x1,y1),N(x2,y2)为图象上另一点,且满足$\overrightarrow{OM}$•$\overrightarrow{ON}$=0,即x1x2+y1y2=0;分别举反例或证明A、B、C中的函数不成立,D中的余弦函数满足题意.
解答 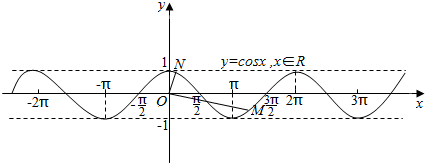 解:根据题意,直角坐标系xOy中,设函数y=f(x)图象上任一点M(x1,y1),
解:根据题意,直角坐标系xOy中,设函数y=f(x)图象上任一点M(x1,y1),
N(x2,y2)为图象上另一点,且$\overrightarrow{OM}$•$\overrightarrow{ON}$=0,
∴$\overrightarrow{OM}$•$\overrightarrow{ON}$=x1x2+y1y2=0;
对于A,任取函数y=2x+1图象上一点M(-1,1),设N(x,y),
则应满足-x+2x+1=0,结合函数的图象知该方程无解,∴A中函数不成立;
对于B,任取函数y=log3(x-2)图象上一点M(3,0),设N(x,y),
则应满足3x=0,则x=0,这与函数的定义域(2,+∞)矛盾,
∴N点不存在,即B中函数不成立;
对于C,x1x2+y1y2=x1x2+$\frac{4}{{{x}_{1}x}_{2}}$≥2或≤-2,∴$\overrightarrow{OM}$•$\overrightarrow{ON}$=x1x2+y1y2=0不成立,
即C中函数一定不成立;
对于D,根据余弦函数的图象,
在函数图象上任取一点M,都可以在图象上找到一点N,
满足$\overrightarrow{OM}$•$\overrightarrow{ON}$=0,∴D中的函数满足题意.
故选:D.
点评 本题考查了新定义的函数的应用问题,也考查了转化思想的应用问题,考查了数形结合思想的应用问题,是综合性题目.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
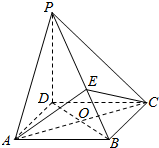 如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,O为AC与BD的交点,E为棱PB上一点,证明:平面EAC⊥平面PBD.
如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,O为AC与BD的交点,E为棱PB上一点,证明:平面EAC⊥平面PBD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com