练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    从装有2个红球和2个白球的红袋内任取两个球,那么下列事件中,对立事件的是(   )
    A．至少有一个白球;都是白球B．至少有一个白球;至少有一个红球
    C．恰好有一个白球;恰好有2个白球D．至少有1个白球;都是红球
    D

    试题分析：解：对于B，“至少有1个白球”发生时，“至少有1个红球”也会发生，,比如恰好一个白球和一个红球，故B不对立,对于D，“至少有1个白球”说明有白球，白球的个数可能是1或2，而“都是红球”说明没有白球，白球的个数是0，这两个 事件不能同时发生，且必有一个发生，故B是对立的；对于C，恰有1个白球，恰有2个白球是互拆事件，它们虽然不能同时发生但是还有可能恰好没有白球的情况，因此它们不对立；对于A，至少有1个白球和都是白球能同时发生，故它们不互拆，更谈不上对立了,故选D
    点评：本题考查了随机事件当中“互拆”与“对立”的区别与联系，属于基础题．互拆是对立的前提，对立是两个互拆事件当中，必定有一个要发生．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    甲乙丙三位同学独立的解决同一个问题，已知三位同学能够正确解决这个问题的概率分别为、、，则有人能够解决这个问题的概率为
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    俗话说：“三个臭皮匠，顶个诸葛亮”，某校三位学生参加数学省举行的数学团体竞赛，对于其中一题，他们各自解出的概率分别是，由于发扬团队精神，此题能解出的概率是        ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    如右图，在正方形内有一扇形（见阴影部分），扇形对应的圆心是正方形的一顶点，半径为正方形的边长。在这个图形上随机撒一粒黄豆，它落在扇形外正方形内的概率为            。（用分数表示）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    甲乙两班进行消防安全知识竞赛，每班出3人组成甲乙两支代表队，首轮比赛每人一道必答题，答对则为本队得1分，答错不答都得0分，已知甲队3人每人答对的概率分别为，乙队每人答对的概率都是．设每人回答正确与否相互之间没有影响，用表示甲队总得分．
    （I）求随机变量的分布列及其数学期望E（）；
    （Ⅱ）求在甲队和乙队得分之和为4的条件下，甲队比乙队得分高的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    甲、乙、丙三人独立破译同一份密码，已知甲、乙、丙各自破译出密码的概率分别为、、，且他们是否破译出密码互不影响，若三人中只有甲破译出密码的概率为．
    （1）求的值．
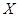    （2）设甲、乙、丙三人中破译出密码的人数为，求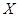的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    ）袋中装有大小相同的黑球、白球和红球共10个。已知从袋中任意摸出1个球，得到黑球的概率是；从袋中任意摸出2个球，至少得到1个白球的概率是
    （1）求袋中各色球的个数；
    （2）从袋中任意摸出3个球，记得到白球的个数为ξ，求随机变量ξ的分布列及数学期望Eξ和方差Dξ；

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    某同学在高考报志愿时，报了4所符合自己分数和意向的高校，若每一所学校录取的概率为，则这位同学被其中一所学校录取的概率为            ；

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    设随机变量X的分布列P＝(＝1，2，3，4，5)．
    (1)求常数的值；
    (2)求P；
    (3)求

    查看答案和解析>>

    同步练习册答案