练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知长方体从同一顶点出发的三条棱长分别为，且成等差数列．若其对角线长为，则的最大值为________．


     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若i为虚数单位，图中复平面内点Z表示复数z，则表示复数的点是(　　)

    A．E       B．F      C．G    D．H

     


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若当n→+∞时，无限趋近于一个常数A，则A可用定积分表示为                                                             （    ）

        A．        B．          C．       D．　　　　　　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    命题“若，则”的逆否命题是

    A．若，则     B．若，则

    C．若，则     D．若，则

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知为坐标原点，向量，．若平面区域由所有满足（，）的点组成，则能够把区域的周长和面积同时分为相等的两部分的曲线是(   )

    A．   B．    C．       D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某供货商拟从码头发货至其对岸的两个商场，处，通常货物先由处船运至之间的中转站，再利用车辆转运．如图，码头与两商场，的距离相等，两商场间的距离为千米，且．若一批货物从码头至处的运费为100元/千米，这批货到后需分别发车2辆、4辆转运至、处，每辆汽车运费为25元/千米．设该批货总运费为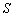元．

    （Ⅰ）写出关于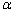的函数关系式，并指出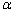的取值范围；

    （Ⅱ）当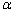为何值时，总运费最小？并求出的最小值．

     


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    复数z=（为虚数单位）在复平面内对应的点所在象限为（    ）

      A．第一象限        B．第二象限      C．第三象限      D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数.

    （1） 求的单调区间与极值；

    （2）是否存在实数，使得对任意的，当时恒有成立．若存在，求的范围，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于函数f(x)=|sin2x|有下列命题:

    ①函数f(x)的最小正周期是;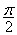

    ②函数f(x)是偶函数;

    ③函数f(x)的图象关于直线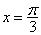对称;

    ④函数f(x)在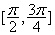上为减函数.

    其中正确命题的序号是(    )

    A.②③                                                                            B.②④  C.①③    D.①②

    查看答案和解析>>

    同步练习册答案