
如图, ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, ,
, 分别是
分别是 ,
, 的中点,
的中点, .
.
(1)证明: ;
;
(2)证明: ;
;
(3)假设这是个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果鱼游到四棱锥 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.

(1)参考解析;(2)参考解析;(3) 
【解析】
试题分析:(1)由于点E是A1C是的中点,点O是BC的中点,连接OE,OA,由三角形的中位线可得OE∥BB1,并且OE=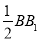 .又
.又 ∥
∥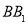 ,并且
,并且 .所以EO与DA平行且相等.所以四边形EOAD是平行四边形.所以DE∥AO.即可得到结论.
.所以EO与DA平行且相等.所以四边形EOAD是平行四边形.所以DE∥AO.即可得到结论.
(2)由 是母线,所以
是母线,所以 平面ABC.所以可得
平面ABC.所以可得 ,又BC是圆得直径,所以
,又BC是圆得直径,所以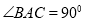 .由此可得结论.
.由此可得结论.
(3)由 ,即可得到
,即可得到 面
面 .即
.即 .所以
.所以 .设圆的半径为r,圆柱的高为h,所以
.设圆的半径为r,圆柱的高为h,所以 .圆柱的体积为
.圆柱的体积为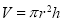 .所以鱼被捕的概率为
.所以鱼被捕的概率为 .
.
(1)证明:连结 ,
, ,
,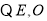 分别为
分别为 的中点,∴
的中点,∴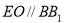 .
.
又 ,且
,且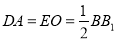 .∴四边形
.∴四边形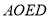 是平行四边形,
是平行四边形,
即 .∴
.∴ . 4分
. 4分
(2) 证明: ,
, 为圆柱
为圆柱 的母线,所以
的母线,所以
因为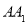 垂直于圆
垂直于圆 所在平面,故
所在平面,故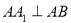 ,
,
又 是底面圆
是底面圆 的直径,所以
的直径,所以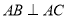 ,
, ,所以
,所以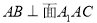 ,
,
由 ,所以
,所以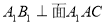 . 8分
. 8分
(3)【解析】
鱼被捕的概率等于四棱锥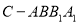 与圆柱
与圆柱 的体积比,
的体积比,
由 ,且由(1)知
,且由(1)知 .∴
.∴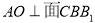 ,
,
∴  ,∴
,∴ .
.
因 是底面圆
是底面圆 的直径,得
的直径,得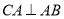 ,且
,且 ,
,
∴ ,即
,即 为四棱锥的高.设圆柱高为
为四棱锥的高.设圆柱高为 ,底半径为
,底半径为 ,
,
则 ,
, ,
,
∴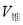 :
:
 ,即
,即
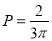 . 12分
. 12分
考点:1.线面平行.2.线面垂直.3.体积的计算.


科目:高中数学 来源:2013-2014学年福建省龙岩市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,若输入m的值为8,则输出s的值为( )

A. 4 B. 6 C. 8 D. 16
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高三高考压轴理科数学试卷(解析版) 题型:填空题
小明在做一道数学题目时发现:若复数
 ,
, (其中
(其中 ), 则
), 则 ,
, ,根据上面的结论,可以提出猜想: z1·z2·z3= .
,根据上面的结论,可以提出猜想: z1·z2·z3= .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高三高考压轴理科数学试卷(解析版) 题型:选择题
如图,在△ABC中,AB=3,AC=5,若O为△ABC的外心,则 的值是(( )
的值是(( )

A.4 B. 8 C.6
B. 8 C.6 D.6
D.6
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高三高考压轴文科数学试卷(解析版) 题型:选择题
若变量 满足约束条件
满足约束条件 且
且 的最大值为
的最大值为 ,最小值为b,则
,最小值为b,则 的值是( )
的值是( )
A.10 B.20 C.4 D.12

查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高考考前模拟理科数学试卷(解析版) 题型:解答题
如图,平面 平面
平面 ,四边形
,四边形 为矩形,
为矩形, .
.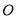 为
为 的中点,
的中点, .
.

(1)求证: ;
;
(2)若 时,求二面角
时,求二面角 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com