Question

18．已知x，y是[0，2]上的两个随机数，则满足x•y∈[0，1]的概率为$\frac{1+2ln2}{4}$．

Answer 1

分析 根据几何概型的概率公式，结合积分的应用求出对应区域的面积进行计算即可．

解答 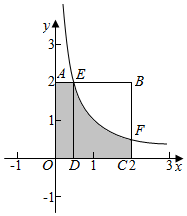解：∵x，y是[0，2]上的两个随机数，
∴$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$，对应的区域为正方形面积S=2×2=4，
当x≠0时，由x•y∈[0，1]得0≤xy≤1，
即y≤$\frac{1}{x}$，
作出不等式组对应的平面区域如图：
则阴影部分的面积S=$\frac{1}{2}×2+{∫}_{\frac{1}{2}}^{2}\frac{1}{x}dx$=1+lnx|${\;}_{\frac{1}{2}}^{2}$=1+ln2-ln$\frac{1}{2}$=1+2ln2，
则满足x•y∈[0，1]的概率为P=$\frac{1+2ln2}{4}$，
故答案为：$\frac{1+2ln2}{4}$

点评 本题主要考查几何概型的概率的计算，根据不等式的关系进行转化，利用数形结合以及积分的应用求出对应区域的面积是解决本题的关键．