
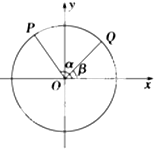
 如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于P,Q两点,已知点P的坐标为$({-\frac{3}{5},\frac{4}{5}})$
如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于P,Q两点,已知点P的坐标为$({-\frac{3}{5},\frac{4}{5}})$分析 (1)由点P的坐标为$({-\frac{3}{5},\frac{4}{5}})$,可得sinα=$\frac{4}{5}$,cosα=$-\frac{3}{5}$,tanα=$-\frac{4}{3}$,sin2α=2sinαcosα,cos2α=2cos2α-1,代入$\frac{sin2α+cos2α+1}{1+tanα}$即可得出.
(2)由$\overrightarrow{OP}•\overrightarrow{OQ}$=0,可得$β=α-\frac{π}{2}$,代入cos(α+β)=$cos(2α-\frac{π}{2})$=sin2α,即可得出.
解答 解:(1)∵点P的坐标为$({-\frac{3}{5},\frac{4}{5}})$,∴sinα=$\frac{4}{5}$,cosα=$-\frac{3}{5}$,
∴tanα=$-\frac{4}{3}$,sin2α=2sinαcosα=2×$\frac{4}{5}×(-\frac{3}{5})$=-$\frac{24}{25}$,cos2α=2cos2α-1=2×$(-\frac{3}{5})^{2}$-1=-$\frac{7}{25}$.
∴$\frac{sin2α+cos2α+1}{1+tanα}$=$\frac{-\frac{24}{25}-\frac{7}{25}+1}{1-\frac{4}{3}}$=$\frac{18}{25}$;
(2)∵$\overrightarrow{OP}•\overrightarrow{OQ}$=0,∴$β=α-\frac{π}{2}$,
∴cos(α+β)=$cos(2α-\frac{π}{2})$=sin2α=-$\frac{24}{25}$.
点评 本题考查了同角三角函数基本关系式、倍角公式、诱导公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{10}^{5}$•C${\;}_{10}^{3}$•C${\;}_{10}^{2}$ | B. | C${\;}_{10}^{5}$•C${\;}_{5}^{3}$•C${\;}_{2}^{2}$ | ||
| C. | C${\;}_{5}^{2}$•C${\;}_{10}^{3}$ | D. | C${\;}_{10}^{5}$•C${\;}_{4}^{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{1}{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com