
���� �ٰ�����$\overline{AP}$��$\overline{AQ}$�ֱ��������εı߳���$\overrightarrow{AB}��\overrightarrow{AC}$��ʾ�����$��\overrightarrow{AP}+\overrightarrow{AQ}��^{2}$����$\overline{AP}$+$\overline{AQ}$�Ĵ�С����
������֪�ɵ�$\overrightarrow{AD}•\overrightarrow{BC}=0$��Ȼ��֤����$\overline{AP}$+$\overline{AQ}$��•$\overrightarrow{BC}$=0�ô𰸣�
��� 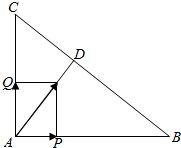 �ٽ⣺������ɵã�$\overrightarrow{AP}=\frac{\overrightarrow{AB}}{{c}^{2}}��\overrightarrow{AQ}=\frac{\overrightarrow{AC}}{{b}^{2}}$��
�ٽ⣺������ɵã�$\overrightarrow{AP}=\frac{\overrightarrow{AB}}{{c}^{2}}��\overrightarrow{AQ}=\frac{\overrightarrow{AC}}{{b}^{2}}$��
��$��\overrightarrow{AP}+\overrightarrow{AQ}��^{2}=��\frac{\overrightarrow{AB}}{{c}^{2}}+\frac{\overrightarrow{AC}}{{b}^{2}}��^{2}$=$\frac{|\overrightarrow{AB}{|}^{2}}{{c}^{4}}+2\frac{1}{{c}^{2}{b}^{2}}\overrightarrow{AB}•\overrightarrow{AC}+\frac{|\overrightarrow{AC}{|}^{2}}{{b}^{4}}$
=$\frac{1}{{c}^{2}}+\frac{1}{{b}^{2}}=\frac{{a}^{2}}{{c}^{2}+{b}^{2}}$��
��$|\overrightarrow{AP}+\overrightarrow{AQ}|=\sqrt{\frac{{a}^{2}}{{c}^{2}+{b}^{2}}}=\frac{a}{{c}^{2}+{b}^{2}}\sqrt{{c}^{2}+{b}^{2}}$��
��֤������AD��BC����$\overrightarrow{AD}•\overrightarrow{BC}=0$��
�֣�$\overline{AP}$+$\overline{AQ}$��•$\overrightarrow{BC}$=��$\frac{\overrightarrow{AB}}{{c}^{2}}+\frac{\overrightarrow{AC}}{{b}^{2}}$��•��$\overrightarrow{AC}-\overrightarrow{AB}$��
=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{{c}^{2}}-\frac{|\overrightarrow{AB}{|}^{2}}{{c}^{2}}+\frac{|\overrightarrow{AC}{|}^{2}}{{b}^{2}}-\frac{\overrightarrow{AC}•\overrightarrow{AB}}{{b}^{2}}$
=$-\frac{{c}^{2}}{{c}^{2}}+\frac{{b}^{2}}{{b}^{2}}=0$��
��$\overline{AP}$+$\overline{AQ}$�ķ�����$\overline{AD}$�ķ�����ͬ��
���� ���⿼���������κ��е�Ӧ�ã����������������ϵĵ�λ���������������ӷ��������������η������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��\frac{1}{3}$ | B�� | $\frac{1}{3}$ | C�� | -$\frac{1}{3}$ | D�� | ��$\frac{\sqrt{2}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
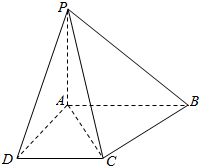 ��ͼ����P-ABCD�У�PB=PC������ABCD��ֱ�����Σ�AB��DC����ABC=60�㣬DC=1��AD=$\sqrt{3}$��
��ͼ����P-ABCD�У�PB=PC������ABCD��ֱ�����Σ�AB��DC����ABC=60�㣬DC=1��AD=$\sqrt{3}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com