
分析 要求圆的方程,就要求出圆心和半径.先求圆心:利用中点坐标公式求出AB的中点,求出垂直平分线的斜率,写出垂直平分线的方程,根据圆的性质可知圆心一定在弦AB的垂直平分线上,与直线x-2y-3=0联立求出圆心坐标,再求半径:根据两点间的距离公式求出圆心与A的距离即为圆的半径,利用圆心和半径写出圆的标准方程即可.
解答 解:由点A(-2,3),B(-2,-5),中点坐标公式求出AB的中点坐标为(-2,-1),AB的垂直的直线的斜率为0,
所以AB的垂直平分线是y=-1,
因为圆心是两直线的交点,联立得$\left\{\begin{array}{l}y=-1\\ x-2y-3=0\end{array}\right.$,
解得$\left\{\begin{array}{l}x=1\\ y=-1\end{array}\right.$,所以圆心坐标O为(1,-1);
所以AO的长度等于圆的半径,则半径r2=(-2-1)2+(3+1)2=25,
所以圆的方程为(x-1)2+(y+1)2=25
故答案为:(x-1)2+(y+1)2=25.
点评 考查学生灵活运用圆的性质解决实际问题,要求学生会利用两个点求中点坐标和所在直线的斜率,掌握两直线垂直时斜率满足的条件,会根据圆心和半径写出圆的标准方程.


 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | B. | -$\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
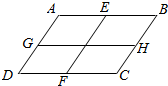 已知E,F,G,H分别是四边形ABCD四条边AB,CD,AD,BC的中点,求$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{AD}$+$\overrightarrow{DC}$=2($\overrightarrow{EF}$+$\overrightarrow{GH}$)
已知E,F,G,H分别是四边形ABCD四条边AB,CD,AD,BC的中点,求$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{AD}$+$\overrightarrow{DC}$=2($\overrightarrow{EF}$+$\overrightarrow{GH}$)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com