
| A�� | $\sqrt{2}$x��y=0 | B�� | x��$\sqrt{2}$y=0 | C�� | 2x��y=0 | D�� | x��2y=0 |
���� ͨ����Բ��˫���ߵķ��̿ɵø��Ե������ʣ����ý��ۣ�
��� �⣺����ԲC1�ķ���Ϊ$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��
����ԲC1��������e1=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$��
��˫����C2�ķ���Ϊ$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1��
��˫����C2��������e2=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}$��
��C1��C2��������֮��Ϊ$\frac{{\sqrt{3}}}{2}$��
��$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$•$\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}$=$\frac{\sqrt{3}}{2}$��
��$\frac{3}{4}$=$[1-��\frac{b}{a}��^{2}][1+��\frac{b}{a}��^{2}]$=1-$��\frac{b}{a}��^{4}$��
�֡�a��b��0����$\frac{b}{a}$=$\frac{1}{\sqrt{2}}$��
��ѡ��B��
���� ���⿼������Բ�����������⣬�����������������ע����ⷽ���Ļ��ۣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
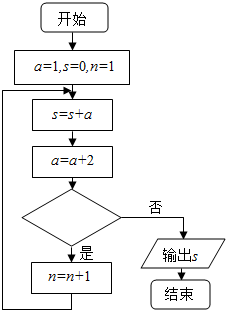 �Ķ���ͼ��ʾ�ij����ͼ��������Ӧ�ij���������Ľ��s=9����ͼ��������Ӧ����д�������ǣ�������
�Ķ���ͼ��ʾ�ij����ͼ��������Ӧ�ij���������Ľ��s=9����ͼ��������Ӧ����д�������ǣ�������| A�� | n��2 | B�� | n��3 | C�� | n��4 | D�� | a��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��$\frac{1}{3}$] | B�� | ��$\frac{1}{3}$��1�� | C�� | ��0��$\frac{1}{3}$�� | D�� | [$\frac{1}{3}$��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com