
【题目】在平面直角坐标系![]() 中曲线
中曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程以及直线
的普通方程以及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)将曲线![]() 向左平移2个单位,再将曲线
向左平移2个单位,再将曲线![]() 上的所有点的横坐标缩短为原来的
上的所有点的横坐标缩短为原来的![]() ,得到曲线
,得到曲线![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
【答案】(1)![]() ;
;![]() ; (2)
; (2)![]() .
.
【解析】
(1)曲线![]() 的参数方程化简消参后得到普通方程,利用
的参数方程化简消参后得到普通方程,利用![]() ,对直线
,对直线![]() 的极坐标方程进行化简,得到
的极坐标方程进行化简,得到![]() 的直角坐标方程;
的直角坐标方程;
(2)根据变换规则,得到变换后的曲线![]() 的方程,写出其参数方程,从而得到曲线
的方程,写出其参数方程,从而得到曲线![]() 上任一点的坐标,利用点到直线的距离公式,结合正弦型函数的值域,得到最小值.
上任一点的坐标,利用点到直线的距离公式,结合正弦型函数的值域,得到最小值.
(1)曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)
为参数)
所以![]() ,两式平方后相加得
,两式平方后相加得![]() ,
,
即曲线![]() 的普通方程为:
的普通方程为:![]() .
.
直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
即![]()
![]() ,
,
因为![]() ,
,
所以直线![]() 的直角坐标方程为:
的直角坐标方程为:![]()
(2)曲线![]() :
:![]() 向左平移2个单位,
向左平移2个单位,
得到![]() ,
,
再将曲线![]() 上的所有点的横坐标缩短为原来的
上的所有点的横坐标缩短为原来的![]()
得到![]() ,
,
即曲线![]() ;
;
所以曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
设曲线![]() 上任一点
上任一点![]() ,
,
则点![]() 到直线
到直线![]() 的距离为:
的距离为:
则 (其中
(其中![]() ),
),
当![]() 时,
时,![]() 取最小值,为
取最小值,为![]()
所以点![]() 到直线
到直线![]() 的距离的最小值为
的距离的最小值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立的极坐标系中,直线
轴的正半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为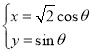 (
(![]() 为参数).
为参数).
(1)写出直线![]() 及曲线
及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 且平行于直线
且平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() ,求点
,求点![]() 的轨迹及其直角坐标方程.
的轨迹及其直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教师调查了![]() 名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
男生 | 女生 | 总计 | |
购买数学课外辅导书超过 |
|
|
|
购买数学课外辅导书不超过 |
|
|
|
总计 |
|
|
|
(Ⅰ)根据表格中的数据,是否有![]() 的把握认为购买数学课外辅导书的数量与性别相关;
的把握认为购买数学课外辅导书的数量与性别相关;
(Ⅱ)从购买数学课外辅导书不超过![]() 本的学生中,按照性别分层抽样抽取
本的学生中,按照性别分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人询问购买原因,求恰有
人询问购买原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
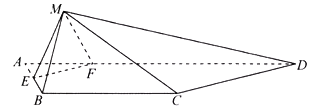
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=1,AD=2,点E、F分别在线段AB、AD上,且EF∥CD,将△AEF沿EF折起到△MEF的位置,并使平面MEF⊥平面BCDFE,得到几何体M﹣BCDEF,则折叠后的几何体的体积的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学棋艺协会定期举办“以棋会友”的竞赛活动,分别包括“中国象棋”、“围棋”、“五子棋”、“国际象棋”四种比赛,每位协会会员必须参加其中的两种棋类比赛,且各队员之间参加比赛相互独立;已知甲同学必选“中国象棋”,不选“国际象棋”,乙同学从四种比赛中任选两种参与.
(1)求甲参加围棋比赛的概率;
(2)求甲、乙两人参与的两种比赛都不同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》是央视首档全民参与的诗词节目,节目以“赏中华诗词,寻文化基因,品生活之美”为宗旨.每一期的比赛包含以下环节:“个人追逐赛”、“攻擂资格争夺赛”和“擂主争霸赛”,其中“擂主争霸赛”由“攻擂资格争夺赛”获胜者与上一场擂主进行比拼.“擂主争霸赛”共有九道抢答题,抢到并答对者得一分,答错则对方得一分,率先获得五分者即为该场擂主.在《中国诗词大会》的某一期节目中,若进行“擂主争霸赛”的甲乙两位选手每道抢答题得到一分的概率都是为0.5,则抢答完七道题后甲成为擂主的概率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com