
分析 (1)设计划B每个月的投资金额构成的数列为{an},则{an}是以a1=100为首项,200为公差的等差数列,从2015年初至2017年末共存了20个月,共投资金额79200,设X为投资股票79200元的获利金额,
则依题意可得X的取值为39600元,-6600元,分别求出相应的概率,由此能求出计划B到2016年底的收益的期望值.
(2)计划A每个月的投资金额构成的数列是一个常数列{bn},bn=1500n,设计划A投资2年的本息总和为Tn,q=1.005,则Tn=1500(q24+q23+q22+…+q)=39195,求出计划A的收益率,由此能求出结果.
解答 解:(1)设计划B每个月的投资金额构成的数列为{an},
则依题意可知{an}是以a1=100为首项,200为公差的等差数列,
∴从2015年初至2017年末共存了20个月,共投资金额:
Sn=24×1000+$\frac{24(24-1)×200}{2}$=79200,
设X为投资股票79200元的获利金额,
则依题意可得X的取值为39600元,-6600元,
P(X=39600)=$\frac{1}{4}$,P(X=-6600)=$\frac{3}{4}$,
∴X的分布列为:
| X | 39600 | -6600 |
| P | $\frac{1}{4}$ | $\frac{3}{4}$ |
点评 本题考查离散型随机变量的分布列及数学期望的求法及应用,是中档题,解题时要认真审题,注意等差数列、等比数列的性质的合理运用.


科目:高中数学 来源: 题型:解答题
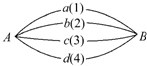 如图,从A地到B地设置了4条不同的网络线路,它们通过的最大信息量分别为1,2,3,4,现从中任取三条网线连通A,B两地(三条网线可通过的信息总量即三条网线各自的最大信息量之和).
如图,从A地到B地设置了4条不同的网络线路,它们通过的最大信息量分别为1,2,3,4,现从中任取三条网线连通A,B两地(三条网线可通过的信息总量即三条网线各自的最大信息量之和).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
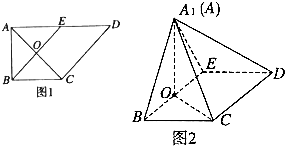 如图1,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图2.
如图1,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com