
分析 (1)设P(x,y),由题意利用斜率计算公式可得:kPA•kPB=t,化为:tx2-y2=tm2,对t与0的大小关系分类讨论即可得出.
(2)当t=$\frac{1}{2}$,m=2$\sqrt{2}$时,曲线C的方程化为:$\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{4}$=1.设过点(-4,0)的直线l的方程为:y=k(x+4),E(x1,y1),F(x2,y2),线段EF的中点M(x0,y0).把直线l的方程代入双曲线化为:(1-2k2)x2-16k2x-32k2-8=0,利用根与系数的关系、中点坐标公式可得线段EF的中点M(x0,y0).由于中点落在区域|x|+|y|≤1内,可得|x0|+|y0|≤1,通过分类讨论解出即可得出.
解答 解:(1)设P(x,y),由题意可得:kPA•kPB=$\frac{y}{x+m}$$•\frac{y}{x-m}$=t,
化为:tx2-y2=tm2.
当t>0时,化为:$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{t{m}^{2}}$=1,表示焦点在x轴上的双曲线;
当t<0时,化为:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{-t{m}^{2}}$=1,表示焦点在x轴或y轴上的椭圆.
(2)当t=$\frac{1}{2}$,m=2$\sqrt{2}$时,曲线C的方程化为:$\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{4}$=1.
设过点(-4,0)的直线l的方程为:y=k(x+4),E(x1,y1),F(x2,y2),
线段EF的中点M(x0,y0).
把直线l的方程代入双曲线化为:(1-2k2)x2-16k2x-32k2-8=0,△>0,
即:256k4+4(1-2k2)(32k2+8)>0,化为2k2+1>0.
∴x1+x2=$\frac{16{k}^{2}}{1-2{k}^{2}}$,x1•x2=$\frac{-32{k}^{2}-8}{1-2{k}^{2}}$,
∴x0=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{8{k}^{2}}{1-2{k}^{2}}$,y0=k(x0+4)=$\frac{4k}{1-2{k}^{2}}$.
∵线段EF的中点落在区域|x|+|y|≤1内,
∴$\frac{8{k}^{2}}{|1-2{k}^{2}|}$+$\frac{4|k|}{|1-2{k}^{2}|}$≤1,
①|k|$≥\frac{\sqrt{2}}{2}$时,化为:6k2+4k+1≤0,无解;
②$0<k<\frac{\sqrt{2}}{2}$时,化为:10k2+4k-1≤0,解得0<k≤$\frac{-2+\sqrt{14}}{10}$;
③-$\frac{\sqrt{2}}{2}$<k<0时,化为:10k2-4k-1≤0,解得$\frac{2-\sqrt{14}}{10}$≤k<0.
④k=0时也成立.
综上可得:直线EF的斜率的取值范围是$[\frac{2-\sqrt{14}}{10},\frac{-2+\sqrt{14}}{10}]$.
点评 本题考查了椭圆的标准方程及其性质、一元二次方程的根与系数的关系、中点坐标公式、不等式的解法、斜率计算公式,考查了分类讨论方法、推理能力与计算能力,属于难题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
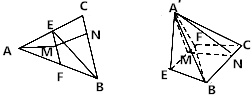 如图,已知等边△ABC中,E,F分别为AB,AC边的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF-CB,M为EF中点.
如图,已知等边△ABC中,E,F分别为AB,AC边的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF-CB,M为EF中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
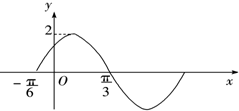 函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.
函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-2,x≥0}\\{-2x+1,x<0}\end{array}\right.$,
已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-2,x≥0}\\{-2x+1,x<0}\end{array}\right.$,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com