
分析 an=-2SnSn-1化简可得$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,且$\frac{1}{{S}_{1}}$=2,从而可判断数列{$\frac{1}{{S}_{n}}$}是以2为首项,2为公差的等差数列,从而求得.
解答 解:∵an=-2SnSn-1,
∴Sn-Sn-1=-2SnSn-1,
∴$\frac{1}{{S}_{n-1}}$-$\frac{1}{{S}_{n}}$=-2,
即$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,且$\frac{1}{{S}_{1}}$=2,
故数列{$\frac{1}{{S}_{n}}$}是以2为首项,2为公差的等差数列,
∴$\frac{1}{{S}_{n}}$=2+2(n-1)=2n,
故Sn=$\frac{1}{2n}$,
故S200=$\frac{1}{400}$,
故答案为:$\frac{1}{400}$.
点评 本题考查了数列的性质的判断与应用,同时考查了整体思想与转化思想的应用及构造法的应用.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
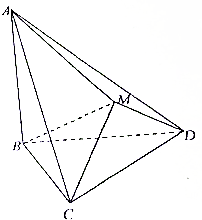 如图,△BCD与△MCD都是正三角形,平面MCD⊥平面BCD,AB⊥平面BCD.
如图,△BCD与△MCD都是正三角形,平面MCD⊥平面BCD,AB⊥平面BCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 16 | C. | 12 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com